Tải ngay
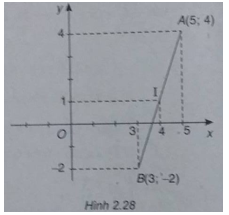
Bài 2.27 trang 92 Sách bài tập (SBT) Toán Hình học 10Trong mặt phẳng Oxy cho hai điểm Trong mặt phẳng Oxy cho hai điểm A(5;4) và B(3;-2). Một điểm M di động trên trục hoành Ox. Tìm giá trị nhỏ nhất của \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right|\) Gợi ý làm bài (h.2.28)
Gọi I là trung điểm của đoạn AB, ta có I(4;1) Vì \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \) nên \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = 2\left| {\overrightarrow {MI} } \right|\) nhỏ nhất khi giá trị của đoạn IM nhỏ nhất. Điểm M chạy trên trục Ox nên có tọa độ dạng M(x; 0). Do đó: \(\left| {\overrightarrow {IM} } \right| = \sqrt {{{(x - 4)}^2} + 1} \ge 1\) Dấu “=” xảy ra khi x = 4. Vậy giá trị nhỏ nhất của \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right|\) là 2 khi M có tọa độ là M(4;0) Sachbaitap.net
Xem lời giải SGK - Toán 10 - Xem ngay >> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 2: Tích vô hướng của hai vec tơ
|
