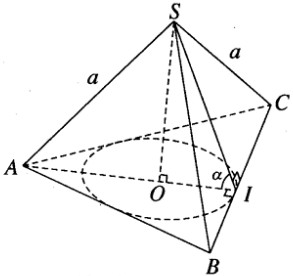
Bài 2.3 trang 50 sách bài tập (SBT) – Hình học 12.Hình nón đỉnh S có đường tròn đáy nội tiếp tam giác đều ABC gọi là hình nón nội tiếp hình nón đã cho. Hãy tính diện tích xung quanh của hình nón này theo a và . Cho S.ABC là hình chóp tam giác đều có các cạnh bên bằng a và có góc giữa các mặt bên và mặt phẳng đáy là \(\alpha \). Hình nón đỉnh S có đường tròn đáy nội tiếp tam giác đều ABC gọi là hình nón nội tiếp hình nón đã cho. Hãy tính diện tích xung quanh của hình nón này theo a và \(\alpha \) . Hướng dẫn làm bài:
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = SB = SC = a và \(\widehat {SIO} = \alpha \). Đặt OI = r, SO = h, ta có AO = 2r và \(\left\{ {\matrix{{h = r\tan \alpha } \cr {{a^2} = {h^2} + 4{r^2}} \cr} } \right.\) (vì SA2 = SO2 + AO2 ) Do đó \({a^2} = {r^2}{\tan ^2}\alpha + 4{r^2} = {r^2}({\tan ^2}\alpha + 4)\) Vậy \(r = {a \over {\sqrt {{{\tan }^2}\alpha + 4} }}\) Hình nón nội tiếp có đường sinh là : \(l = SI = {r \over {\cos \alpha }} = {a \over {\cos \alpha \sqrt {{{\tan }^2}\alpha + 4} }}\) Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là: \({S_{xq}} = \pi rl = \pi .{a \over {\sqrt {{{\tan }^2}\alpha + 4} }}.{a \over {\cos \alpha \sqrt {{{\tan }^2}\alpha + 4} }} = {{\pi {a^2}} \over {\cos \alpha ({{\tan }^2}\alpha + 4)}}\) Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 1. Khái niệm về mặt tròn xoay
|
-
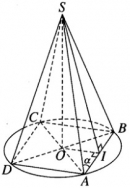
Bài 2.4 trang 50 sách bài tập (SBT) – Hình học 12.
Cho hình chóp tứ giác đều S.ABCD có chiều cao SO = h và góc . Tính diện tích xung quanh của hình nón đỉnh S và có đường tròn đáy ngoại tiếp hình vuông ABCD của hình chóp.
-
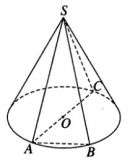
Bài 2.5 trang 50 sách bài tập (SBT) – Hình học 12.
Chứng minh rằng trong một khối nón tròn xoay, góc ở đỉnh là góc lớn nhất trong số các góc được tạo nên bởi hai đường sinh của khối nón đó.
-
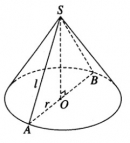
Bài 2.6 trang 50 sách bài tập (SBT) – Hình học 12.
Cho khối nón có bán kính đáy r = 12 cm và có góc ở đỉnh là . Hãy tính diện tích của thiết diện đi qua hai đường sinh vuông góc với nhau.
-
Bài 2.7 trang 50 sách bài tập (SBT) – Hình học 12.
Cho mặt phẳng (P). Gọi A là một điểm nằm trên (P) và B là một điểm nằm ngoài (P) sao cho hình chiếu H của B trên (P) không trùng với A.

 Tải ngay
Tải ngay