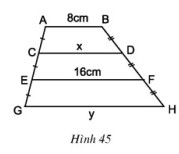
Bài 26, 27, 28 trang 80 SGK Toán 8 tập 1 - Luyện tậpBài 26, 27, 28 trang 80 SGK Toán 8 tập 1 - Luyện tập. Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD ở I , cắt AC ở K . Bài 26 trang 80 SGK Toán lớp 8 tập 1 Câu hỏi: Tính \(x, y\) trên hình \(45\), trong đó \(AB // CD // EF // GH.\)
Phương pháp Áp dụng tính chất: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy. Lời giải: +) Tính x: Xét tứ giác ABFE, có: AB // EF nên tứ giác ABFE là hình thang Hình thang ABFE có: CA = CE nên C là trung điểm của AE DB = DF nên D là trung điểm của BF ⇒ CD là đường trung bình của hình thang ABFE
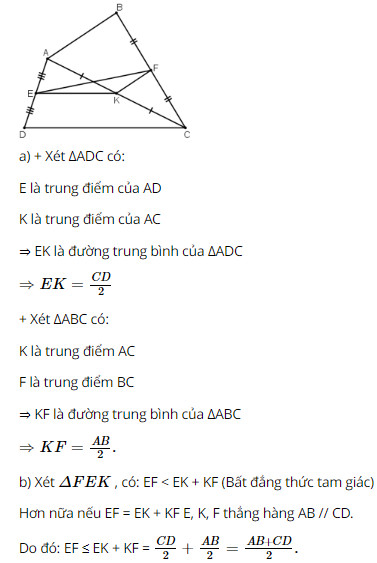
Bài 27 trang 80 SGK Toán lớp 8 tập 1 Câu hỏi: Cho tứ giác \(ABCD.\) Gọi \(E, F, K\) theo thứ tự là trung điểm của \(AD, BC, AC.\) a) So sánh các độ dài \(EK\) và \(CD, KF\) và \(AB.\) b) Chứng minh rằng \(EF ≤ \dfrac{AB+CD}{2}\). Phương pháp: Áp dụng: - Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác. - Trong tam giác tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại. - Định lí: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy. Lời giải:
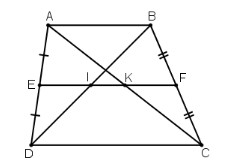
Bài 28 trang 80 SGK Toán lớp 8 tập 1 Câu hỏi: Cho hình thang \(ABCD\) (\(AB // CD\)), \(E\) là trung điểm của \(AD,\) \(F\) là trung điểm của \(BC.\) Đường thẳng \(EF\) cắt \(BD\) ở \(I,\) cắt \(AC\) ở \(K.\) a) Chứng minh rằng \(AK = KC, BI = ID.\) b) Cho \(AB = 6\,cm, CD = 10\,cm.\) Tính các độ dài \(EI, KF, IK.\) Phương pháp: Cho hình thang \(ABCD\) (\(AB // CD\)), \(E\) là trung điểm của \(AD,\) \(F\) là trung điểm của \(BC.\) Đường thẳng \(EF\) cắt \(BD\) ở \(I,\) cắt \(AC\) ở \(K.\) a) Chứng minh rằng \(AK = KC, BI = ID.\) b) Cho \(AB = 6\,cm, CD = 10\,cm.\) Tính các độ dài \(EI, KF, IK.\) Lời giải:
a) + Xét hình thang ABCD có: E là trung điểm của AD (gt) F là trung điểm của BC (gt) ⇒ EF là đường trung bình của hình thang ABCD. ⇒ EF // AB // CD + Xét ΔABC có: F là trung điểm BC (gt) FK // AB (cmt) ⇒ K là trung điểm của AC hay AK = KC. + Xét ΔABD có: E là trung điểm của AD (gt) EI // AB (cmt) ⇒ I là trung điểm của BD hay BI = ID b) + Xét hình thang ABCD có: EF là đường trung bình của hình thang ABCD.
Sachbaitap.com
Xem thêm tại đây:
Chương I. Tứ giác
|
-

Bài 29, 30, 31 trang 83 SGK Toán 8 tập 1 - Dựng hình bằng thước và com-pa. Dựng hình thang
Bài 29, 30, 31 trang 83 SGK Toán 8 tập 1 - Dựng hình bằng thước và com-pa. Dựng hình thang. Bài Dựng (∆ABC) vuông tại (A), biết cạnh huyền (BC = 4,cm), góc nhọn.
-

Bài 32, 33, 34 trang 83 SGK Toán 8 tập 1 - Luyện tập
Bài 32, 33, 34 trang 83 SGK Toán 8 tập 1 - Luyện tập. Bài 34 Dựng hình thang (ABCD), biết D = 90 độ, đáy (CD = 3cm), cạnh bên (AD = 2cm), cạnh bên (BC = 3cm).
-

Bài 35, 36, 37, 38 trang 87, 88 SGK Toán 8 tập 1 - Đối xứng trục
Bài 35, 36, 37 trang 87, bài 38 trang 88 SGK Toán 8 tập 1 - Đối xứng trục. Bài 38 Thực hành. Cắt một tấm bìa hình tam giác cân, một tấm bìa hình thang cân. Hãy cho biết đường nào là trục đối xứng của mỗi hình, sau đó gấp mỗi tấm bìa để kiểm tra lại điều đó.
-

Bài 39, 40, 41, 42 trang 88 SGK Toán 8 tập 1 - Luyện tập
Bài 39, 40, 41, 42 trang 88 SGK Toán 8 tập 1 - Luyện tập. Bài 39 a) Cho hai điểm (A, B) thuộc cùng một nửa mặt phẳng có bờ là đường thẳng (d) (h.(60)). Gọi (C) là điểm đối xứng với (A) qua (d.) Gọi (D) là giao điểm của đường thẳng (d) và đoạn thẳng (BC.) Gọi (E) là điểm bất kì của đường thẳng (d) ((E) khác (D)).

 Tải ngay
Tải ngay