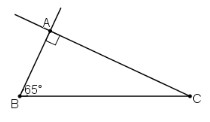
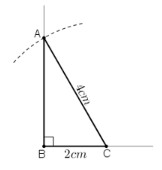
Bài 29, 30, 31 trang 83 SGK Toán 8 tập 1 - Dựng hình bằng thước và com-pa. Dựng hình thang

Bài 29 trang 83 SGK Toán lớp 8 tập 1

Câu hỏi:

Dựng \(∆ABC\) vuông tại \(A\), biết cạnh huyền \(BC = 4\,cm\), góc nhọn \(\widehat{B}={65^0}\) 

Phương pháp:

Dựng \(∆ABC\) vuông tại \(A\), biết cạnh huyền \(BC = a\,cm\), góc nhọn \(\widehat{B}={x^0}\) 

Cách dựng:

- Dựng đoạn thẳng \(BC=a\,cm\)

- Dựng \(\widehat {CBx} = {x^o}\)

- Dựng \(CA\bot Bx\)

Lời giải:

a) Phân tích

Giả sử dựng được ΔABC thỏa mãn yêu cầu đề bài.

Đoạn thẳng BC dựng được vì đã biết độ dài.

Khi đó điểm A là giao điểm của:

+ Tia Bx tạo với đoạn thẳng BC góc 65º

+ Đường thẳng qua C và vuông góc với tia Bx vừa dựng.

b) Cách dựng:

- Dựng đoạn thẳng BC = 4cm.

- Dựng tia Bx tạo với BC một góc 65º.

- Dựng đường thẳng a qua C và vuông góc với Bx.

- Bx cắt a tại A.

ΔABC là tam giác cần dựng.

c) Chứng minh: ΔABC vừa dựng vuông tại A, góc B = 65º và BC = 4cm.

d) Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện đề bài.

Bài 30 trang 83 SGK Toán 8 tập 1

Câu hỏi:

Dựng tam giác \(ABC\) vuông tại \(B\), biết cạnh huyền \(AC = 4\,cm\), cạnh góc vuông \(BC = 2\,cm.\)

Phương pháp:

Dựng tam giác \(ABC\) vuông tại \(B\), biết cạnh huyền \(AC = b\,cm\), cạnh góc vuông \(BC = a\,cm.\)

Cách dựng: 

- Dựng \(\widehat {xBy} = {90^0}\). Trên tia \(Bx\) lấy điểm \(C\) sao cho \(BC = a\,cm.\)

- Dựng cung tròn \((C; b\,cm)\) và cung tròn này cắt tia \(By\) tại \(A.\)

- Nối \(A\) với \(C\) ta được  \(∆ABC\) là tam giác cần dựng.

Lời giải:

a) Phân tích:

Giả sử dựng được ΔABC thỏa mãn yêu cầu.

Ta dựng được đoạn BC vì biết BC = 2cm.

Khi đó điểm A là giao điểm của:

+ Tia Bx vuông góc với BC

+ Cung tròn tâm C bán kính 4cm.

b) Cách dựng:

+ Dựng đoạn thẳng BC = 2cm.

+ Dựng tia Bx vuông góc với cạnh BC.

+ Dựng cung tròn tâm C, bán kính 4cm. Cung tròn cắt tia Bx tại A.

Kẻ AC ta được ΔABC cần dựng.

c) Chứng minh

ΔABC có góc B = 90º, BC = 2cm.

A thuộc cung tròn tâm C bán kính 4cm nên AC = 4cm.

Vậy ΔABC thỏa mãn yêu cầu đề bài

d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.

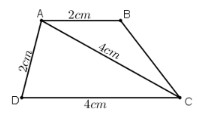
Bài 31 trang 83 SGK Toán 8 tập 1

Câu hỏi:

Dựng hình thang \(ABCD\; (AB // CD)\), biết \(AB = AD = 2\,cm,\) \( AC = DC = 4\,cm.\)

Phương pháp:

Áp dụng phương pháp dựng tam giác, hình thang.

Lời giải:

a) Phân tích :

Giả sử dựng được hình thang ABCD thỏa mãn yêu cầu đề bài.

Tam giác ADC dựng được vì biết ba cạnh của tam giác.

Điểm B phải thỏa mãn hai điều kiện :

+ B nằm trên tia Ax song song với CD

+ B cách A một đoạn 2cm.

b) Cách dựng:

+ Dựng tam giác ADC có AD = 2cm, AC = 4cm, CD = 4cm.

+ Dựng tia Ax song song với CD và nằm trên cùng một nửa mặt phẳng chứa điểm C bờ là đường thẳng AD.

+ Trên tia Ax lấy điểm B sao cho AB = 2cm.

Kẻ BC ta được hình thang ABCD cần dựng.

c) Chứng minh

Tứ giác ABCD là hình thang vì AB // CD.

Hình thang ABCD có AB = AD = 2cm, AC = BC = 4cm thỏa mãn yêu cầu đề bài

d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn yêu cầu của đề bài.

Sachbaitap.com