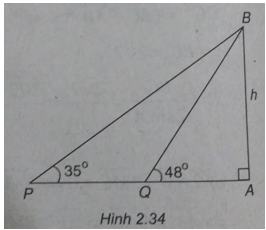
Bài 2.64 trang 105 Sách bài tập (SBT) Toán Hình học 10

Bình chọn:

4.3 trên 3 phiếu

Hai chiếc tàu thủy P và Q cách nhau 300m.

Hai chiếc tàu thủy P và Q cách nhau 300m. Từ P và Q thẳng hàng với chân A của tháp hải đẳng AB trên bờ biển người ta nhìn chiều cao AB của tháp dưới các góc \(\widehat {BPA} = {35^o}\) và \(\widehat {BQA} = {48^ô}\)

a)Tính BQ;

b)Tính chiều cao của tháp.

Gợi ý làm bài

a) (Xem hình 2.34)

Ta có: \(\widehat {PBQ} = {48^ \circ } - {35^ \circ } = {13^ \circ }\)

Trong tam giác BPQ ta có:

\({{BQ} \over {\sin P}} = {{PQ} \over {\sin B}} \Leftrightarrow {{BQ} \over {\sin {{35}^ \circ }}} = {{300} \over {\sin {{13}^ \circ }}}\)

Do đó: \(BQ = {{300.\sin {{35}^ \circ }} \over {\sin {{13}^ \circ }}} \approx 764,935(m)\)

b) Chiều cao của tháp là

\(\eqalign{
& AB = BQ\sin {48^ \circ } \cr
& \approx 764,935.\sin {48^ \circ } \approx 568,457(m) \cr} \)

Sachbaitap.net

Báo lỗi - Góp ý

Xem lời giải SGK - Toán 10 - Xem ngay

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, hoàn trả học phí nếu học không hiệu quả.