Bài 46, 47, 48, 49 trang 92, 93 SGK Toán 8 tập 1 - Luyện tậpBài 46, 47, 48, 49 trang 92, 93 SGK Toán 8 tập 1 - Luyện tập. Bài 48 Tứ giác (ABCD) có (E, F, G, H) theo thứ tự là trung điểm của các cạnh (AB, BC, CD, DA.) Tứ giác (EFGH) là hình gì? Vì sao? Bài 46 trang 92 SGK Toán lớp 8 tập 1 Câu hỏi: Các câu sau đúng hay sai ? a. Hình thang có hai cạnh đáy bằng nhau là hình bình hành. b. Hình thang có hai cạnh bên song song là hình bình hành. c. Tứ giác có hai cạnh đối bằng nhau là hình bình hành. d. Hình thang có hai cạnh bên bằng nhau là hình bình hành. Phương pháp: Áp dụng dấu hiệu nhận biết hình bình hành. Lời giải: a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bằng nhau nên là hình bình hành theo dấu hiệu nhận biết 3 b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa) c) Sai. Ví dụ tứ giác ABCD ở dưới có AB = CD nhưng không phải hình bình hành.
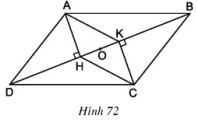
Bài 47 trang 93 SGK Toán lớp 8 tập 1 Câu hỏi: Cho hình \(72\), trong đó \(ABCD\) là hình bình hành.
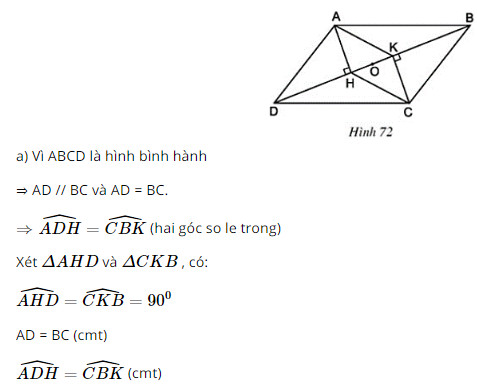
a.Chứng minh rằng \(AHCK\) là hình bình hành. b. Gọi \(O\) là trung điểm của \(HK\). Chứng minh rằng ba điểm \(A, O, C\) thẳng hàng Phương pháp: a. Áp dụng: Dấu hiệu nhận biết hình bình hành: Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành. b. Áp dụng: Tính chất hình bình hành: Hai đường chéo cắt nhau tại trung điểm của mỗi đường. Lời giải:
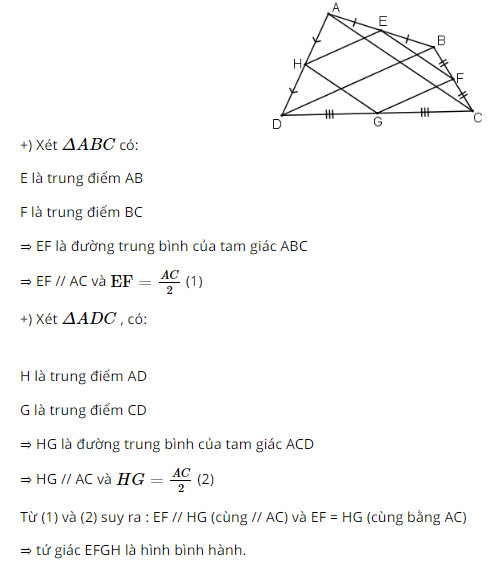
⇒ ΔAHD = ΔCKB (cạnh huyền, góc nhọn) ⇒ AH = CK Ta có: AH ⊥ BD; CK ⊥ BD ⇒ AH // CK Tứ giác AHCK có AH // CK, AH = CK nên là hình bình hành. b) Hình bình hành AHCK có O là trung điểm HK nên O là trung điểm của AC ⇒ A, C, O thẳng hàng. Bài 48 trang 93 SGK Toán lớp 8 tập 1 Câu hỏi: Tứ giác \(ABCD\) có \(E, F, G, H\) theo thứ tự là trung điểm của các cạnh \(AB, BC, CD, DA.\) Tứ giác \(EFGH\) là hình gì ? Vì sao ? Phương pháp: Áp dụng: +) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy. +) Dấu hiệu nhận biết hình bình hành: Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành. Lời giải:
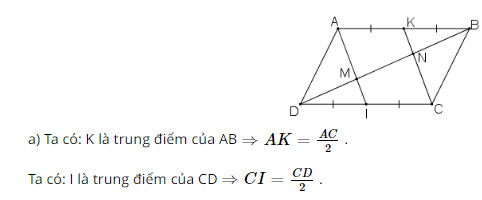
Bài 49 trang 93 SGK Toán lớp 8 tập 1 Câu hỏi: Cho hình bình hành \(ABCD.\) Gọi \(I, K\) theo thứ tự là trung điểm của \(CD, AB.\) Đường chéo \(BD\) cắt \(AI, CK\) theo thứ tự ở \(M\) và \(N.\) Chứng minh rằng: a) \(AI // CK\) b) \(DM = MN = NB\) Phương pháp: Áp dụng: +) Hình bình hành có các cặp cạnh đối song song và bằng nhau. +) Dấu hiệu nhận biết hình bình hành: Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành. +) Định lí: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba Lời giải:
Vì ABCD là hình bình hành ⇒ AB // CD hay AK // CI và AB = CD hay AK = CI Xét tứ giác AKCI có AK // CI và AK = CI ⇒ AKCI là hình bình hành. b) Vì AKCI là hình bình hành ⇒ AI//KC hay MI//NC. Xét ΔDNC có: I là trung điểm DC IM // NC ⇒">⇒⇒ M là trung điểm DN ⇒">⇒⇒ DM = MN (1) Xét ΔBAM có: K là trung điểm AB KN//AM ⇒">⇒⇒ N là trung điểm BM ⇒">⇒⇒ MN = NB (2) Từ (1) và (2) suy ra DM = MN = NB. Sachbaitap.com
Xem thêm tại đây:
Chương I. Tứ giác
|
-

Bài 50, 51, 52, 53 trang 95, 96 SGK Toán 8 tập 1 - Đối xứng tâm
Bài 50 trang 95,bài 51, 52, 53 trang 96 SGK Toán 8 tập 1 - Đối xứng tâm. Bài 53 Cho hình (82), trong đó (MD // AB) và (ME // AC). Chứng minh rằng điểm (A) đối xứng với điểm (M) qua điểm (I).
-

Bài 54, 55, 56, 57 trang 96 SGK Toán 8 tập 1 - Luyện tập
Bài 54, 55, 56, 57 trang 96 SGK Toán 8 tập 1 - Luyện tập. Bài 55 Cho hình bình hành (ABCD), (O) là giao điểm của hai đường chéo. Một đường thẳng đi qua (O) cắt các cạnh (AB) và (CD) theo thứ tự ở (M) và (N). Chứng minh rằng điểm (M) đối xứng với điểm (N) qua (O).
-

Bài 58, 59, 69, 61 trang 99 SGK Toán 8 tập 1 - Hình chữ nhật
Bài 58, 59, 69, 61 trang 99 SGK Toán 8 tập 1 - Hình chữ nhật. Bài 61 Cho tam giác (ABC), đường cao (AH). Gọi (I) là trung điểm của (AC, E) là điểm đối xứng với (H) qua (I). Tứ giác (AHCE) là hình gì ? Vì sao ?
-
Bài 62, 63, 64, 65, 66 trang 99, 100 SGK Toán 8 tập 1 - Luyện tập
Bài 62 trang 99,bài 63, 64, 65, 66 trang 100 SGK Toán 8 tập 1 - Luyện tập. Bài 65 Tứ giác (ABCD) có hai đường chéo vuông góc với nhau. Gọi (E, F, G, H) theo thứ tự là trung điểm của các cạnh (AB, BC, CD, DA). Tứ giác (EFGH) là hình gì? Vì sao?

 Tải ngay
Tải ngay