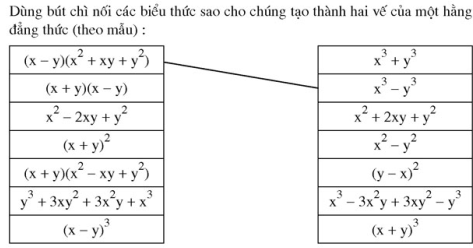
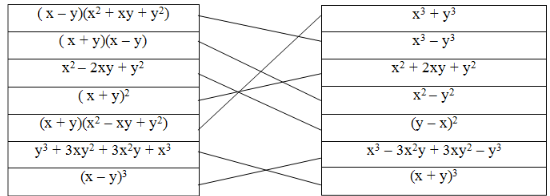
Bài 30, 31, 32, 33, 34, 35, 36, 37, 38 trang 16, 17 SGK Toán 8 tập 1 - Những hằng đẳng thức đáng nhớ (tiếp) - Luyện tập

Bài 30 trang 16 SGK Toán lớp 8 tập 1

Câu hỏi:

Rút gọn các biểu thức sau:

\(\,\,\left( {x + 3} \right)({x^2} - 3x + 9) - (54 + {x^3})\)

\(\left( {2x + y} \right)(4{x^2} - 2xy + {y^2}) - \left( {2x - y} \right)(4{x^2} + 2xy + {y^2})\)

Phương pháp:

a. 

Áp dụng: Hằng đẳng thức tổng hai lập phương, quy tắc phá dấu ngoặc.

\({A^3} + {B^3} = \left( {A + B} \right)({A^2} - AB + {B^2})\)

b. 

Áp dụng: Hằng đẳng thức tổng hai lập phương, hiệu hai lập phương, quy tắc phá dấu ngoặc.

\({A^3} + {B^3} = \left( {A + B} \right)({A^2} - AB + {B^2})\)

\({A^3} - {B^3} = \left( {A - B} \right)({A^2} + AB + {B^2})\)

Lời giải:

a) (x + 3)(x² – 3x + 9) – (54 + x³)

= x³ + 3³ – (54 + x³) (Áp dụng HĐT (6) với A = x và B = 3)

= x³ + 27 – 54 – x³

= –27

b) (2x + y)(4x² – 2xy + y²) – (2x – y)(4x² + 2xy + y²)

= (2x + y)[(2x)² – 2x.y + y²] – (2x – y)[(2x)² + 2x.y + y²]

= [(2x)³ + y³] – [(2x)³ – y³]

= (2x)³ + y³ – (2x)³ + y³

= 2y³

Bài 31 trang 16 SGK Toán lớp 8 tập 1

Câu hỏi:

Chứng minh rằng:

a) \({a^3} + {b^3} = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right)\)

b) \({a^3} - {b^3} = {\left( {a - b} \right)^3} + 3ab\left( {a - b} \right)\)

Áp dụng: Tính \({a^3} + {b^3}\) , biết \(a . b = 6\) và \(a + b = -5.\)

Phương pháp:

- Biến đổi vế phải của đẳng thức về vế trái đẳng thức.

- Áp dụng các hằng đẳng thức đáng nhớ: lập phương của một tổng hoặc một hiệu, tổng (hiệu) hai lập phương, nhân đơn thức với đa thức.

Lời giải:

a) Biến đổi vế phải ta được:

(a + b)³ – 3ab(a + b)

= a³ + 3a²b + 3ab² + b³ – 3a²b – 3ab²

= a³ + b³

Vậy a³ + b³ = (a + b)³ – 3ab(a + b)

b) Biến đổi vế phải ta được:

(a – b)³ + 3ab(a – b)

= a³ – 3a²b + 3ab² – b³ + 3a²b – 3ab²

= a³ – b³

Vậy a³ – b³ = (a – b)³ + 3ab(a – b)

– Áp dụng: Với ab = 6, a + b = –5, ta được:

a³ + b³ = (a + b)³ – 3ab(a + b) = (–5)³ – 3.6.(–5) = –5³ + 3.6.5 = –125 + 90 = –35

Bài 32 trang 16 SGK Toán lớp 8 tập 1

Câu hỏi:

Phương pháp:

Áp dụng: Hằng đẳng thức tổng hai lập phương.

\({A^3} + {B^3} = \left( {A + B} \right)({A^2} - AB + {B^2})\)

Lời giải:

Bài 33 trang 16 SGK Toán lớp 8 tập 1

Câu hỏi:

a. Tính:

\(\eqalign{
& \,\,{\left( {2 + xy} \right)^2} \cr} \)

b. \(\eqalign{
& \,\,{\left( {5 - 3x} \right)^2} \cr} \)

c.  \(\eqalign{& \,\,(5 - {x^2})(5 + {x^2}) \cr} \)

d. \(\eqalign{
& \,\,{\left( {5x - 1} \right)^3} \cr} \)

e. \(\eqalign{
& \,\,\left( {2x - y} \right)(4{x^2} + 2xy + {y^2}) \cr} \)

h. \(\eqalign{
& \,\,\left( {x + 3} \right)({x^2} - 3x + 9) \cr} \)

Phương pháp:

a.

Áp dụng hằng đẳng thức đáng nhớ để khai triển biểu thức đó.

\({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)

b. 

Áp dụng hằng đẳng thức đáng nhớ để khai triển biểu thức đó.

\({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)

c. 

Áp dụng hằng đẳng thức đáng nhớ để khai triển biểu thức đó.

\({A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\)

d. 

Áp dụng hằng đẳng thức đáng nhớ để khai triển biểu thức đó.

\({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\)

e.

Áp dụng hằng đẳng thức đáng nhớ để khai triển biểu thức đó.

\({A^3} - {B^3} = \left( {A - B} \right)({A^2} + AB + {B^2})\)

h. 

Áp dụng hằng đẳng thức đáng nhớ để khai triển biểu thức đó.

\({A^3} + {B^3} = \left( {A + B} \right)({A^2} - AB + {B^2})\)

Lời giải:

a) (a + b)² – (a – b)²

= [(a + b) – (a – b)].[(a + b) + (a – b)]

= [a + b - a + b].[a + b + a - b]

= 2b.2a

= 4ab

b) (a + b)³ – (a – b)³ – 2b³

= (a³ + 3a²b + 3ab² + b³) – (a³ – 3a²b + 3ab² – b³) – 2b³ (Áp dụng HĐT (4) và (5))

= a³ + 3a²b + 3ab² + b³ – a³ + 3a²b – 3ab² + b³ – 2b³

= (a³ – a³) + (3a²b + 3a²b) + (3ab² – 3ab²) + (b³ + b³ – 2b³)

= 6a²b

c) (x + y + z)² – 2.(x + y + z).(x + y) + (x + y)²

= [(x + y + z) – (x + y)]² (Áp dụng HĐT (2) với A = x + y + z ; B = x + y)

= z².

Bài 35 trang 17 SGK Toán lớp 8 tập 1

Câu hỏi:

a. \(\eqalign{
& \,\,{34^2} + {66^2} + 68.66 \cr} \)

b. \(\eqalign{
& \,\,{74^2} + {24^2} - 48.74 \cr} \)

Phương pháp:

a.

Áp dụng hằng đẳng thức: bình phương của một tổng.

\(1)\,{\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)

b. 

Áp dụng hằng đẳng thức: bình phương của một hiệu.

\(2)\,{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)

Lời giải:

a) 34² + 68.66 + 66²

= 34² + 2.34.66 + 66²

= (34 + 66)²

= 100²

= 10 000

b) 74² – 48.74 + 24²

= 74² – 2.74.24 + 24²

= (74 – 24)²

= 50²

= 2 500

Bài 36 trang 17 SGK Toán lớp 8 tập 1

Câu hỏi:

a. \(\,\,{x^2} + 4x + 4\) tại \(x = 98\);

b. \(\,\,{x^3} + 3{x^2} + 3x + 1\) tại \(x = 99\)

Phương pháp:

a. Áp dụng hằng đẳng thức bình phương của một tổng để rút gọn biểu thức, sau đó thay giá trị của \(x\) để tính giá trị của biểu thức.

\({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)

b. 

Áp dụng hằng đẳng thức lập phương của một tổng để rút gọn biểu thức, sau đó thay giá trị của \(x\) để tính giá trị của biểu thức.

\({\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\)

Lời giải:

a) x² + 4x + 4

= x² + 2.x.2 + 2²

= (x + 2)²

Tại x = 98, giá trị biểu thức bằng (98 + 2)² = 100² = 10000

b) x³ + 3x² + 3x + 1

= x³ + 3.x².1 + 3.x.1² + 1³

= (x + 1)³

Tại x = 99, giá trị biểu thức bằng (99 + 1)³ = 100³ = 1000000

Bài 37 trang 17 SGK Toán lớp 8 tập 1

Câu hỏi:

Phương pháp:

Áp dụng các hằng đẳng thức đáng nhớ. 

\(1)\,{\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)

\(2)\,{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)

\(3)\,{A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\)

\(4)\,{\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\)

\(5)\,{\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\)

\(6)\,{A^3} + {B^3} = \left( {A + B} \right)({A^2} - AB + {B^2})\)

\(7)\,{A^3} - {B^3} = \left( {A - B} \right)({A^2} + AB + {B^2})\)

Lời giải:

Bài 38 trang 17 SGK Toán lớp 8 tập 1

Câu hỏi:

Chứng minh các đẳng thức sau:

a. \({\left( {a - b} \right)^3} =  - {\left( {b - a} \right)^3}\);

b. \({\left( { - a - b} \right)^2} = {\left( {a + b} \right)^2}\)

Phương pháp:

a. Áp dụng hằng đẳng thức đáng nhớ: lập phương của một hiệu, sử dụng quy tắc dấu ngoặc, ta biến đổi một vế của đẳng thức thành vế còn lại, ta được điều phải chứng minh.

\(5)\,{\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\)

b. 

Áp dụng hằng đẳng thức đáng nhớ: bình phương của một tổng, sử dụng quy tắc dấu ngoặc, ta biến đổi một vế của đẳng thức thành vế còn lại, ta được điều phải chứng minh.

\(1)\,{\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)

Lời giải:

a) Sử dụng tính chất hai số đối nhau:

(a – b)³ = [(–1)(b – a)]³ =(–1)³(b – a)³ = –1.(b – a)³ = –(b – a)³ (đpcm)

b) (–a – b)² = [(– 1).(a + b)]² = (–1)²(a + b)² = 1.(a + b)² = (a + b)² (đpcm) 

Sachbaitap.com