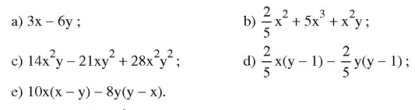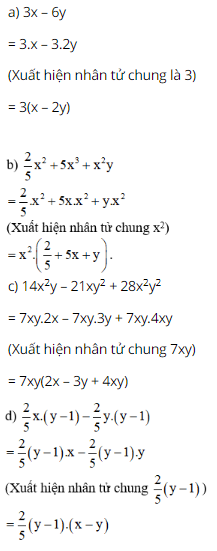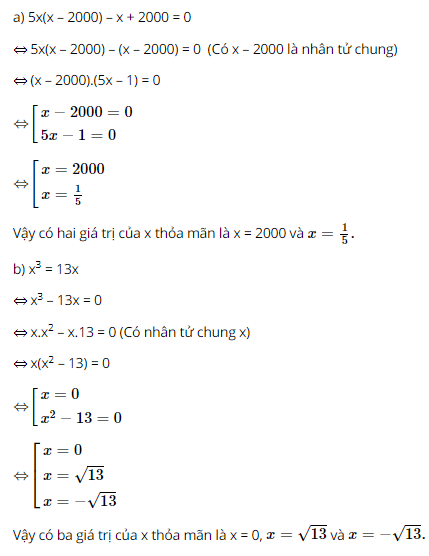Bài 39, 40, 41, 42 trang 19 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chungGiải bài 39, 40, 41, 42 trang 19 SGK Toán 8 tập 1 - Bài Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung. Bài 42. Chứng minh rằng 55^n+1 - 55^n chia hết cho 54 (với n là số tự nhiên). Bài 39 trang 19 SGK Toán lớp 8 tập 1 Câu hỏi: Phân tích các đa thức sau thành nhân tử:
Phương pháp: - Phân tích các hạng tử để xuất hiện nhân tử chung. Lời giải:
e) 10x(x – y) – 8y(y – x) (Nhận thấy x – y = –(y – x) nên ta đổi y – x về x – y) = 10x(x – y) – 8y[–(x – y)] = 10x(x – y) + 8y(x – y) = 2(x – y).5x + 2(x – y).4y (Xuất hiện nhân tử chung 2(x – y)) = 2(x – y)(5x + 4y) * Lưu ý: Nhiều khi, để xuất hiện nhân tử chung, ta cần biến đổi A = –(–A) Bài 40 trang 19 SGK Toán lớp 8 tập 1 Câu hỏi: Tính giá trị biểu thức: a. \(15 . 91,5 + 150 . 0,85\); b. \(x(x - 1) - y(1 - x)\) tại \(x = 2001\) và \(y = 1999.\) Phương pháp: a.- Phân tích các hạng tử để xuất hiện nhân tử chung rồi đặt nhân tử chung ra ngoài. b. - Phân tích các hạng tử để xuất hiện nhân tử chung. Chú ý: \(1-x=-(x-1)\) - Sau khi phân tích đa thức thành nhân tử, ta thay giá trị tương ứng của \(x\) và \(y\) vào biểu thức để tính giá trị của biểu thức đó. Lời giải: a) 15.91,5 + 150.0,85 = 15.91,5 + 15.10.0,85 = 15.91,5 + 15.8,5 = 15(91,5 + 8,5) = 15.100 = 1500 b) x(x – 1) – y(1 – x) = x(x – 1) – y[–(x – 1)] = x(x – 1) + y(x – 1) = (x – 1)(x + y) Tại x = 2001, y = 1999, giá trị biểu thức bằng: (2001 – 1)(2001 + 1999) = 2000.4000 = 8000000 Bài 41 trang 19 SGK Toán lớp 8 tập 1 Câu hỏi: Tìm \(x\), biết: a.\(5x(x -2000) - x + 2000 = 0\); b.\({x^3} - 13x = 0\) Phương pháp: Áp dụng: +) Phương pháp phân tích đa thức thành nhân tử. +) \(A.B=0\) suy ra \(A=0\) hoặc \(B=0\) Lời giải:
Bài 42 trang 19 SGK Toán lớp 8 tập 1 Câu hỏi: Chứng minh rằng \({55^{n + 1}} - {55^n}\) chia hết cho \(54 \) (với \(n\) là số tự nhiên) Phương pháp: Áp dụng - Phân tích đa thức thành nhân tử. - Tính chất chia hết của một tích cho một số. Lời giải: Có : 55n + 1 – 55n = 55n.55 – 55n = 55n(55 – 1) = 55n.54 Vì 54 chia hết cho 54 nên 55n.54 luôn chia hết cho 54 với mọi số tự nhiên n. Vậy 55n + 1 – 55n chia hết cho 54. Sachbaitap.com
Xem thêm tại đây:
Chương I. Phép nhân và phép chia các đa thức
|
-

Bài 43, 44, 45, 46 trang 20, 21 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
Giải bài 43, 44, 45 trang 20, bài 46 trang 21 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức. Bài 46: Tính nhanh: a) 732 - 272 ; b) 372 - 132 ; c) 20022 - 22
-

Bài 47, 48, 49, 50 trang 22, 23 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
Giải bài 47, 48, 49 trang 22, bài 50 trang 23 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử. Bài 49: Tính nhanh: (37,5 . 6,5 - 7,5 . 3,4 - 6,6 . 7,5 + 3,5 . 37,5) ({45^2} + {40^2} - {15^2} + 80.45).
-

Bài 51, 52, 53, 54, 55, 56, 57, 58 trang 24, 25 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp - luyện tập
Bài 51, 52, 53 trang 24, bài 54, 55, 56, 57, 58 trang 25 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp- luyện tập. Bài 52 Chứng minh rằng ((5n + 2)^2- 4) chia hết cho (5) với mọi số nguyên (n).
-

Bài 59, 60, 61, 62 trang 26, 27 SGK Toán 8 tập 1 - Chia đơn thức cho đơn thức
Bài 59 trang 26, bài 60, 61, 62 trang 27 SGK Toán 8 tập 1 -Chia đơn thức cho đơn thức. Bài 62 Tính giá trị của biểu thức (15{x^4}{y^3}{z^2}:5x{y^2}{z^2}) với (x = 2, y = -10, z = 2004)

 Tải ngay
Tải ngay