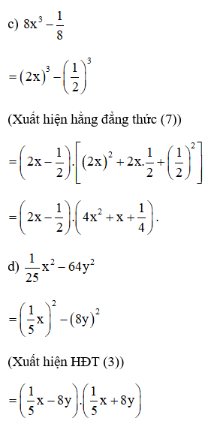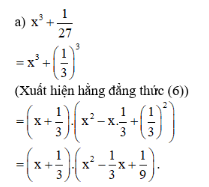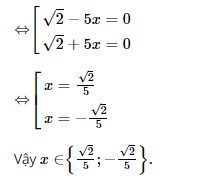Bài 43, 44, 45, 46 trang 20, 21 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thứcGiải bài 43, 44, 45 trang 20, bài 46 trang 21 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức. Bài 46: Tính nhanh: a) 732 - 272 ; b) 372 - 132 ; c) 20022 - 22 Bài 43 trang 20 SGK Toán lớp 8 tập 1 Câu hỏi: Phân tích các đa thức sau thành nhân tử: \({x^2} + 6x + 9\); \(10x - 25 - {x^2}\); \(8{x^3}-\dfrac{1}{8}\); \(\dfrac{1}{25}{x^2} - 64{y^2}\) Phương pháp: Áp dụng hằng đẳng thức đáng nhớ: \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\) Lời giải: a) x2 + 6x + 9 = x2 + 2.x.3 + 32 (Xuất hiện hằng đẳng thức (1)) = (x + 3)2 b) 10x – 25 – x2 = –(–10x + 25 + x2) = –(25 – 10x + x2) = –(52 – 2.5.x + x2) (Xuất hiện hằng đẳng thức (2) trong ngoặc) = –(5 – x)2 Bài 44 trang 20 SGK Toán lớp 8 tập 1 Câu hỏi: Phân tích các đa thức sau thành nhân tử: \({x^3} + \dfrac{1}{27}\); \({\left( {a + b} \right)^3} - {\left( {a - b} \right)^3}\); \({\left( {a + b} \right)^3} + {\left( {a - b} \right)^3}\); \(8{x^3} + 12{x^2}y + 6x{y^2} + {y^3}\) \( - {x^3} + 9{x^2} - 27x + 27.\) Phương pháp: Áp dụng hằng đẳng thức đáng nhớ: Lập phương một hiệu. \(5)\,{\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\) Lời giải:
b) (a + b)3 – (a – b)3 (Xuất hiện hằng đẳng thức (7)) = [(a + b) – (a – b)][(a + b)2 + (a + b).(a – b) + (a – b)2] = (a + b – a + b)(a2 + 2ab + b2 + a2 – b2+ a2 – 2ab + b2) = 2b.(3a2+ b2) c) (a + b)3 + (a – b)3 (Xuất hiện hằng đẳng thức (6)) = [(a + b) + (a – b)][(a + b)2 – (a + b)(a –b) + (a – b)2] = [(a + b) + (a – b)][(a2 + 2ab + b2) – (a2 – b2) + (a2 – 2ab + b2)] = (a + b + a – b)(a2 + 2ab + b2 – a2 + b2 + a2 – 2ab + b2) = 2a.(a2 + 3b2) d) 8x3 + 12x2y + 6xy2 + y3 = (2x)3 + 3.(2x)2.y + 3.2x.y2 + y3 (Xuất hiện hằng đẳng thức (4)) = (2x + y)3 e) –x3 + 9x2 – 27x + 27 = (–x)3 + 3.(–x)2.3 + 3.(–x).32 + 33 (Xuất hiện Hằng đẳng thức (4)) = (–x + 3)3 = (3 – x)3 Bài 45 trang 20 SGK Toán lớp 8 tập 1 Câu hỏi: Tìm \(x\), biết: \(2 - 25x^2= 0\); \(x^2- x + \dfrac{1}{4} = 0\) Phương pháp: - Phân tích các biểu thức ở vế trái thành nhân tử, sau đó áp dụng tính chất: \(A.B = 0 \Rightarrow A=0\) hoặc \(B=0\) - Áp dụng hằng đẳng thức bình phương một hiệu. \(2)\,{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) Lời giải:
Bài 46 trang 21 SGK Toán lớp 8 tập 1 Câu hỏi: Tính nhanh: a) 732 - 272 ; b) 372 - 132 ; c) 20022 - 22 Phương pháp: Áp dụng hằng đẳng thức hiệu hai bình phương để phân tích các đa thức đó thành nhân tử. \(3)\,{A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\) Lời giải: a) 732 – 272 = (73 + 27)(73 – 27) = 100.46 = 4600 b) 372 – 132 = (37 + 13)(37 – 13) = 50.24 = 100.12 = 1200 c) 20022 – 22 = (2002 + 2)(2002 – 2) = 2004 .2000 Sachbaitap.com
Xem thêm tại đây:
Chương I. Phép nhân và phép chia các đa thức
|
-

Bài 47, 48, 49, 50 trang 22, 23 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
Giải bài 47, 48, 49 trang 22, bài 50 trang 23 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử. Bài 49: Tính nhanh: (37,5 . 6,5 - 7,5 . 3,4 - 6,6 . 7,5 + 3,5 . 37,5) ({45^2} + {40^2} - {15^2} + 80.45).
-

Bài 51, 52, 53, 54, 55, 56, 57, 58 trang 24, 25 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp - luyện tập
Bài 51, 52, 53 trang 24, bài 54, 55, 56, 57, 58 trang 25 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp- luyện tập. Bài 52 Chứng minh rằng ((5n + 2)^2- 4) chia hết cho (5) với mọi số nguyên (n).
-

Bài 59, 60, 61, 62 trang 26, 27 SGK Toán 8 tập 1 - Chia đơn thức cho đơn thức
Bài 59 trang 26, bài 60, 61, 62 trang 27 SGK Toán 8 tập 1 -Chia đơn thức cho đơn thức. Bài 62 Tính giá trị của biểu thức (15{x^4}{y^3}{z^2}:5x{y^2}{z^2}) với (x = 2, y = -10, z = 2004)
-
Bài 63, 64, 65, 66 trang 28, 29 SGK Toán 8 tập 1 - Chia đa thức cho đơn thức
Bài 63, 64 trang 28, bài 65, 66 trang 29 SGK Toán 8 tập 1 - Chia đa thức cho đơn thức. Bài 63. Không làm tính chia, hãy xét xem đa thức A có chia hết cho đơn thức B không:

 Tải ngay
Tải ngay