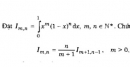Bài 3.18 trang 179 sách bài tập (SBT) - Giải tích 12b) Tính I3 và I5. Đặt \({I_n} = \int\limits_0^{{\pi \over 2}} {{{\sin }^n}xdx} ,n \in {N^*}\) a) Chứng minh rằng \({I_n} = {{n - 1} \over n}{I_{n - 2}},n > 2\) b) Tính I3 và I5. Hướng dẫn làm bài a) Xét với n > 2, ta có: \({I_n} = \int\limits_0^{{\pi \over 2}} {{{\sin }^{n - 1}}x.\sin xdx} \) Dùng tích phân từng phần với và , ta có: \({I_n} = \int\limits_0^{{\pi \over 2}} {{{\sin }^{n - 1}}x\sin xdx}\) \({= - } \cos x{\sin ^{n - 1}}x\left| {\matrix{{{\pi \over 2}} \cr 0 \cr} } \right. + (n - 1)\int\limits_0^{{\pi \over 2}} {{{\sin }^{n - 2}}x{{\cos }^2}xdx} \) \( = (n - 1)\int\limits_0^{{\pi \over 2}} {({{\sin }^{n - 2}}x - {{\sin }^n}x)dx} \) \(= (n - 1){I_{n - 2}} - (n - 1){I_n}\) Vậy \({I_n} = {{n - 1} \over n}{I_{n - 2}}\) b) \({I_3} = {2 \over 3},{I_5} = {8 \over {15}}\) Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 2. Tích phân
|
-
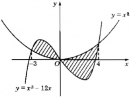
Bài 3.21 trang 184 sách bài tập (SBT) - Giải tích 12
Tính diện tích hình phẳng giới hạn bởi các đường sau:

 Tải ngay
Tải ngay