Tải ngay
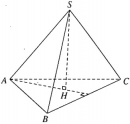
Bài 3.26 trang 153 Sách bài tập (SBT) Hình học 11Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a và có SA = SB = SC = a. Chứng minh: Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a và có SA = SB = SC = a. Chứng minh: a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD) b) Tam giác SBD là tam giác vuông tại S. Giải: a) Gọi O là tâm của hình thoi, ta có \(AC \bot BD\) tại O Vì SA = SC nên \(SO \bot AC\). Do đó AC vuông góc với mặt phẳng (SBD) Ta suy ra mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD). b) Ba tam giác SAC, BAC, DAC bằng nhau ( c.c.c) nên ta suy ra OS = OB = OD. Vậy tam giác SBD vuông tại S. Sachbaitap.com
Xem lời giải SGK - Toán 11 - Xem ngay >> Học trực tuyến Lớp 11 cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng. Cam kết giúp học sinh lớp 11 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 4. Hai mặt phẳng vuông góc
|
-
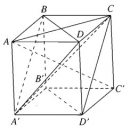
Bài 3.27 trang 153 Sách bài tập (SBT) Hình học 11
a) Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Chứng minh rằng đường thẳng AC’ vuông
-
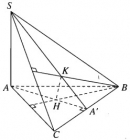
Bài 3.29 trang 153 Sách bài tập (SBT) Hình học 11
Tứ diện SABC có SA vuông góc với mặt phẳng (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC. Chứng minh rằng:
-
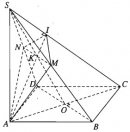
Bài 3.31 trang 153 Sách bài tập (SBT) Hình học 11
Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD).
