-
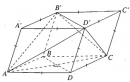
Bài 3.22 trang 152 Sách bài tập (SBT) Hình học 11
Khi mặt phẳng (AA’C’C) vuông góc với mặt phẳng (BB’D’D)?
-
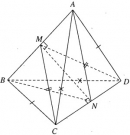
Bài 3.23 trang 152 Sách bài tập (SBT) Hình học 11
Cho tứ diện ABCD có ba cặp cạnh đối diện bằng nhau là AB = CD, AC = BD và AD = BC. Gọi M và N lần lượt là trung điểm của AB và CD.
-
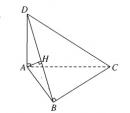
Bài 3.25 trang 152 Sách bài tập (SBT) Hình học 11
Cho tam giác ABC vuông tại B. Một đoạn thẳng AD vuông góc với mặt phẳng (ABC). Chứng minh rằng mặt phẳng (ABD) vuông góc với mặt phẳng (BCD).
-
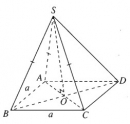
Bài 3.26 trang 153 Sách bài tập (SBT) Hình học 11
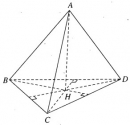
Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a và có SA = SB = SC = a. Chứng minh:
-
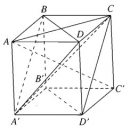
Bài 3.27 trang 153 Sách bài tập (SBT) Hình học 11
a) Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Chứng minh rằng đường thẳng AC’ vuông
-
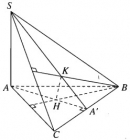
Bài 3.29 trang 153 Sách bài tập (SBT) Hình học 11
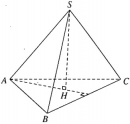
Tứ diện SABC có SA vuông góc với mặt phẳng (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC. Chứng minh rằng:
-
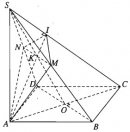
Bài 3.31 trang 153 Sách bài tập (SBT) Hình học 11
Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD).
-
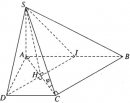
Bài 3.32 trang 154 Sách bài tập (SBT) Hình học 11
a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).

 Tải ngay
Tải ngay