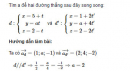Bài 3.33 trang 129 sách bài tập (SBT) – Hình học 12Xét vị trí tương đối của các cặp đường thẳng d và d’ cho bởi các phương trình sau: Xét vị trí tương đối của các cặp đường thẳng d và d’ cho bởi các phương trình sau: a) \(d:{{x + 1} \over 1} = {{y - 1} \over 2} = {{z + 3} \over 3}\) và \(d':{{x - 1} \over 3} = {{y - 5} \over 2} = {{z - 4} \over 2}\) b)\(d:\left\{ {\matrix{{x = t} \cr {y = 1 + t} \cr {z = 2 - t} \cr} } \right.\) và \(d':\left\{ {\matrix{{x = 9 + 2t'} \cr {y = 8 + 2t'} \cr {z = 10 - 2t'} \cr} } \right.\) c) \(d:\left\{ {\matrix{{x = - t} \cr {y = 3t} \cr {z = - 1 - 2t} \cr} } \right.\) và \(d':\left\{ {\matrix{{x = 0} \cr {y = 9} \cr {z = 5t'} \cr} } \right.\) Hướng dẫn làm bài: a) Ta có: \(\overrightarrow {{a_d}} = (1;2;3)\) và \(\overrightarrow {{a_{d'}}} = (3;2;2)\) Suy ra \(\overrightarrow n = \overrightarrow {{a_d}} \wedge \overrightarrow {{a_{d'}}} = ( - 2;7; - 4)\) Ta có \({M_0}( - 1;1; - 2) \in d,{M_0}'(1;5;4) \in {\rm{d' \Rightarrow }}\overrightarrow {{M_0}{M_0}'} = (2;4;6)\) Ta có \(\overrightarrow n .\overrightarrow {{M_0}{M_0}'} = - 4 + 28 - 24 = 0\) . Vậy đường thẳng d và d’ đồng phẳng và khác phương, nên d và d’ cắt nhau. b) Ta có \(\overrightarrow {{a_d}} = (1;1; - 1)\) và \(\overrightarrow {{a_{d'}}} = (2;2; - 2).{M_0}(0;1;2) \in d\) Vì \(\left\{ {\matrix{{\overrightarrow {{a_{d'}}} = 2\overrightarrow {{a_d}} } \cr {{M_0} \notin d'} \cr} } \right.\) (tọa độ M0 không thỏa mãn d’) nên hai đường thẳng d và d’ song song. c) d có vecto chỉ phương \(\overrightarrow {{a_d}} = ( - 1;3; - 2)\) d’ có vecto chỉ phương \(\overrightarrow {{a_{d'}}} = (0;0;5)\) Gọi \(\overrightarrow n = \overrightarrow {{a_d}} \wedge \overrightarrow {{a_{d'}}} = (15;5;0) \ne \overrightarrow 0 \) Ta có \({M_0}(0;0; - 1) \in d\) \(M{'_0}(0;9;0) \in d' \Rightarrow \overrightarrow {{M_0}M{'_0}} = (0;9;1),\overrightarrow n .\overrightarrow {{M_0}M{'_0}} = 45 \ne 0\) Vậy d và d’ là hai đường thẳng chéo nhau. Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 3. Phương trình đường thẳng - SBT Toán 12
|
-
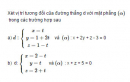
Bài 3.35 trang 129 sách bài tập (SBT) – Hình học 12
Xét vị trí tương đối của đường thẳng d với mặt phẳng trong các trường hợp sau
-
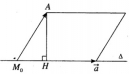
Bài 3.36 trang 130 sách bài tập (SBT) – Hình học 12
Tính khoảng cách từ điểm A(1; 0; 1) đến đường thẳng
-

Bài 3.37 trang 130 sách bài tập (SBT) – Hình học 12
Cho đường thẳng và mặt phẳng : 2x – 2y + z + 3 = 0

 Tải ngay
Tải ngay