Bài 3.35 trang 129 sách bài tập (SBT) – Hình học 12Xét vị trí tương đối của đường thẳng d với mặt phẳng trong các trường hợp sau Xét vị trí tương đối của đường thẳng d với mặt phẳng \((\alpha )\) trong các trường hợp sau a) \(d:\left\{ {\matrix{{x = t} \cr {y = 1 + 2t} \cr {z = 1 - t} \cr} } \right.\) và \((\alpha )\) : x + 2y + z - 3 = 0 b) d: \(\left\{ {\matrix{{x = 2 - t} \cr {y = t} \cr {z = 2 + t} \cr} } \right.\) và \((\alpha )\) : x + z + 5 = 0 c)\(d:\left\{ {\matrix{{x = 3 - t} \cr {y = 2 - t} \cr {z = 1 + 2t} \cr} } \right.\) và \((\alpha )\) : x +y + z -6 = 0 Hướng dẫn làm bài: a) Thay x, y, z trong phương trình tham số của đường thẳng d vào phương trình tổng quát của mặt phẳng \((\alpha )\) ta được: t + 2(1 + 2t) + (1 – t) – 3 = 0 ⟺ 4t = 0 ⟺ t = 0 Vậy đường thẳng d cắt mặt phẳng \((\alpha )\) tại M0(0; 1; 1). b) Thay x, y, z trong phương trình tham số của d vào phương trình tổng quát của \((\alpha )\) ta được: (2 – t) +(2 + t) + 5 = 0 ⟺ 0t = -9 Phương trình vô nghiệm, vậy đường thẳng d song song với \((\alpha )\) c) Thay x, y, z trong phương trình tham số của d vào phương trình tổng quát của \((\alpha )\) ta được: (3 – t) + (2 – t) + (1 + 2t) – 6 = 0 ⟺ 0t = 0 Phương trình luôn thỏa mãn với mọi t. Vậy d chứa trong \((\alpha )\) . Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 3. Phương trình đường thẳng - SBT Toán 12
|
-
Bài 3.36 trang 130 sách bài tập (SBT) – Hình học 12
Tính khoảng cách từ điểm A(1; 0; 1) đến đường thẳng
-

Bài 3.37 trang 130 sách bài tập (SBT) – Hình học 12
Cho đường thẳng và mặt phẳng : 2x – 2y + z + 3 = 0
-
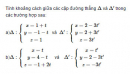
Bài 3.38 trang 130 sách bài tập (SBT) – Hình học 12
Tính khoảng cách giữa các cặp đường thẳng d và d' trong các trường hợp sau:

 Tải ngay
Tải ngay