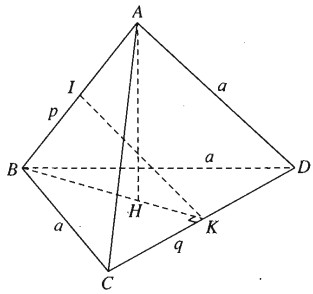
Bài 3.38 trang 162 Sách bài tập (SBT) Hình học 11Tính khoảng cách giữa hai cạnh AB và CD của hình tứ diện ABCD biết rằng Tính khoảng cách giữa hai cạnh AB và CD của hình tứ diện ABCD biết rằng \(AC = BC = A{\rm{D}} = B{\rm{D}} = a\) và \(AB = p,C{\rm{D}} = q\). Giải:
Gọi I và K lần lượt là trung điểm của AB và CD (h.3.80), ta có IK là đoạn vuông góc chung của AB và CD và độ dài đoạn IK là khoảng cách cần tìm: \(I{K^2} = B{K^2} - B{I^2} = B{K^2} - {{{p^2}} \over 4}\) Mà \(B{K^2} = B{C^2} - C{K^2} = {a^2} - {{{q^2}} \over 4}\) Vậy \(I{K^2} = {a^2} - {{{p^2} + {q^2}} \over 4}\) Do đó \(IK = {1 \over 2}\sqrt {4{{\rm{a}}^2} - \left( {{p^2} + {q^2}} \right)} \) Với điều kiện \(4{{\rm{a}}^2} - \left( {{p^2} + {q^2}} \right) > 0\). Sachbaitap.com
Xem lời giải SGK - Toán 11 - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 5. Khoảng cách
|
-
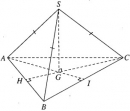
Bài 3.39 trang 162 Sách bài tập (SBT) Hình học 11
Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác đáy ABC.
-
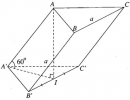
Bài 3.40 trang 162 Sách bài tập (SBT) Hình học 11
Cho hình lăng trụ tam giác ABC.A’B’C’có tất cả các cạnh bên và cạnh đáy đều bằng a. Các cạnh bên của lăng trụ tạo với mặt phẳng đáy góc 60° và hình chiếu vuông góc của đỉnh A lên mặt phẳng (A’B’C’) trùng với trung điểm của cạnh B’C’.
-

Bài 3.41 trang 163 Sách bài tập (SBT) Hình học 11
Trong các mệnh đề sau đây mệnh đề nào đúng? Mệnh đề nào sai?
-

Bài 3.42 trang 163 Sách bài tập (SBT) Hình học 11
a) Qua một điểm, có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.

 Tải ngay
Tải ngay