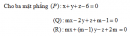Bài 39 trang 124 Sách bài tập Hình học lớp 12 Nâng caoViết phương trình mặt phẳng đi qua điểm Viết phương trình mặt phẳng đi qua điểm M0(1;2;4), cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho \(OA = OB = OC \ne 0.\) Giải Mặt phẳng cần tìm đi qua điểm M0(1;2;4) có phương trình: \(a(x-1)+b(y-2)+c(z-4)=0\) (1) hay \(ax+by+cz=a+2b+4c\) với \(a + 2b + 4c \ne 0\) (theo giả thiết) Từ đó, ta xác định được tọa độ các giao điểm A, B, C là: \(\eqalign{ & A = \left( {{{a + 2b + 4c} \over a};0;0} \right)\cr&B = \left( {0;{{a + 2b + 4c} \over b};0} \right) \cr & C = \left( {0;0;{{a + 2b + 4c} \over c}} \right) \cr} \) Vì OA = OB = OC nên \(O{A^2} = O{B^2} = O{C^2},\) do đó ta có \({{{{\left( {a + 2b + 4c} \right)}^2}} \over {{a^2}}} = {{{{\left( {a + 2b + 4c} \right)}^2}} \over {{b^2}}} = {{{{\left( {a + 2b + 4c} \right)}^2}} \over {{c^2}}}\) Hay \({a^2} = {b^2} = {c^2}\). Có những trường hợp sau xảy ra: +) Nếu a, b, c cùng dấu thì \(a=b=c\) và phương trình (1) trở thành \(x+y+z-7=0\). +) Nếu a, b cùng dấu và khác dấu với c thì \(a=b=-c\). Phương trình (1) trở thành \(x+y-z+1=0\). +) Nếu a, c cùng dấu và khác dấu với c thì \(a=c=-b\). Phương trình (1) trở thành \(x-y+z-3=0\). +) Nếu b, c cùng dấu và khác dấu với a thì \(–a=b=c\). Phương trình (1) trở thành : \(-x+y+z-5=0\). Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 2. Phương trình mặt phẳng
|
-

Bài 43 trang 125 Sách bài tập Hình học lớp 12 Nâng cao
Viết phương trình mặt phẳng trong mỗi trường hợp sau:

 Tải ngay
Tải ngay