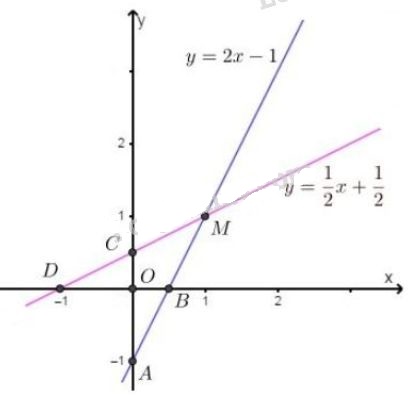
Bài 4, 5, 6 trang 11 SGK Toán 9 tập 2 - Hệ hai phương trình bậc nhất hai ẩnGiải bài 4, 5, 6 trang 11 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Hệ hai phương trình bậc nhất hai ẩn. Bài 6 Đố: Bạn Nga nhận xét: Hai hệ phương trình bậc nhất hai ẩn vô nghiệm thì luôn tương đương với nhau. Bài 4 trang 11 SGK Toán lớp 9 tập 2 Câu hỏi: Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao: a) \(\left\{\begin{matrix} y = 3 - 2x & & \\ y = 3x - 1 & & \end{matrix}\right.\); b) \(\left\{\begin{matrix} y = -\dfrac{1}{2}x+ 3 & & \\ y = -\dfrac{1}{2}x + 1 & & \end{matrix}\right.\); c) \(\left\{\begin{matrix} 2y = -3x & & \\ 3y = 2x & & \end{matrix}\right.\); d) \(\left\{\begin{matrix} 3x - y = 3 & & \\ x - \dfrac{1}{3}y = 1 & & \end{matrix}\right.\) Lời giải: a) Ta có: \(\left\{\begin{matrix} y = 3 - 2x & & \\ y = 3x - 1 & & \end{matrix}\right.\) ⇔ \(\left\{\begin{matrix} y = -2x + 3 \, (d) & & \\ y = 3x - 1 \, (d') & & \end{matrix}\right.\) Ta có \(a = -2, a' = 3\) nên \(a ≠ a'\). Do đó hai đường thẳng \( (d)\) và \((d')\) cắt nhau nên hệ phương trình đã cho có một nghiệm duy nhất. b) Ta có: \(\left\{\begin{matrix} y = -\dfrac{1}{2}x+ 3 \, (d) & & \\ y = -\dfrac{1}{2}x + 1 \, (d') & & \end{matrix}\right.\) Ta có \(a = -\dfrac{1}{2},b = 3 \) và \(a' = -\dfrac{1}{2}, b' = 1\) nên \(a = a', b ≠ b'\). Do đó hai đường thẳng \( (d)\) và \((d')\) song song nên hệ phương trình đã cho vô nghiệm. c) Ta có: \(\left\{\begin{matrix} 2y = -3x & & \\ 3y = 2x & & \end{matrix}\right.\)⇔ \(\left\{\begin{matrix} y = -\dfrac{3}{2}x \, (d) & & \\ y = \dfrac{2}{3}x\, (d') & & \end{matrix}\right.\) Ta có \(a = -\dfrac{3}{2}, a' = \dfrac{2}{3}\) nên \(a ≠ a'\) Do đó hai đường thẳng \( (d)\) và \((d')\) cắt nhau nên hệ phương trình đã cho có một nghiệm duy nhất. d) Ta có: \(\left\{\begin{matrix} 3x - y = 3 & & \\ x - \dfrac{1}{3}y = 1 & & \end{matrix}\right.\) ⇔\(\left\{\begin{matrix} y = 3x - 3 & & \\ \dfrac{1}{3}y = x - 1 & & \end{matrix}\right.\) ⇔ \(\left\{\begin{matrix} y = 3x - 3\, (d) & & \\ y = 3x - 3 \, (d')& & \end{matrix}\right.\) Ta có \(a = 3,\ b = -3 \) và \(a' = 3,\ b' = -3\) nên \(a = a',\ b = b'\). Do đó hai đường thẳng \( (d)\) và \((d')\) trùng nhau nên hệ phương trình đã cho có vô số nghiệm. Bài 5 trang 11 SGK Toán lớp 9 tập 2 Câu hỏi: Đoán nhận số nghiệm của hệ phương trình sau bằng hình học: a) \( \left\{ \matrix{2{\rm{x}} - y = 1 \hfill \cr x - 2y = - 1 \hfill \cr} \right. \); b) \( \left\{ \matrix{2{\rm{x + }}y = 4 \hfill \cr - x + y = 1 \hfill \cr} \right. \) Lời giải: a) Ta có: \(\left\{ \matrix{ +) Vẽ \((d)\): \(y=2x-1\) Cho \(x = 0 \Rightarrow y = -1\), ta được \(A(0; -1)\). Cho \(y = 0 \Rightarrow x = \dfrac{1}{2}\), ta được \(B{\left(\dfrac{1}{2}; 0 \right)}\). Đường thẳng (d) là đường thẳng đi qua hai điểm \(A,\ B\). +) Vẽ \((d')\): \(y=\dfrac{1}{2}x+\dfrac{1}{2}\) Cho \(x = 0 \Rightarrow y = \dfrac{1}{2}\), ta được \(C {\left(0; \dfrac{1}{2} \right)}\). Cho \(y = 0 \Rightarrow x = -1\), ta được \(D = (-1; 0)\). Đường thẳng (d') là đường thẳng đi qua hai điểm \(C,\ D\).
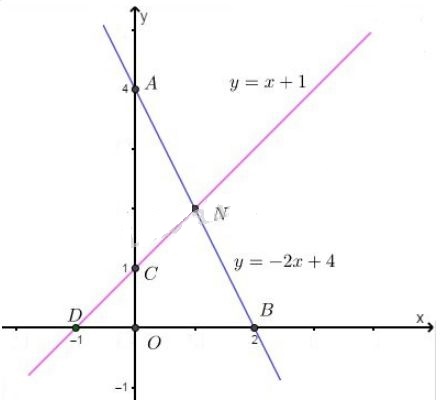
+) Quan sát hình vẽ, ta thấy hai đường thẳng cắt nhau tại điểm có tọa độ \(M( 1, 1)\). Thay \(x = 1, y = 1\) vào các phương trình của hệ ta được: \(\left\{ \begin{array}{l}2x - y = 1\\x - 2y = - 1\end{array} \right.\) \(\Rightarrow\left\{ \begin{array}{l}2.1 - 1 = 1\\1 - 2.1 = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 = 1\\ - 1 = - 1\end{array} \right.\) (luôn đúng) Vậy hệ phương trình có một nghiệm \((x; y) = (1; 1)\). b) Ta có: \(\left\{ \matrix{ +) Vẽ \((d)\): \(y=-2x+4\) Cho \(x = 0 \Rightarrow y = 4\), ta được \(A(0; 4)\). Cho \(y = 0 \Rightarrow x = 2\), ta được \(B(2; 0)\). Đường thẳng (d) là đường thẳng đi qua hai điểm \(A,\ B\). Vẽ \((d')\): \(y=x+1\) Cho \(x = 0 \Rightarrow y = 1\), ta được \(C(0; 1)\). Cho \(y = 0 \Rightarrow x = -1\), ta được \(D(-1; 0)\). Đường thẳng (d') là đường thẳng đi qua hai điểm \(C,\ D\).
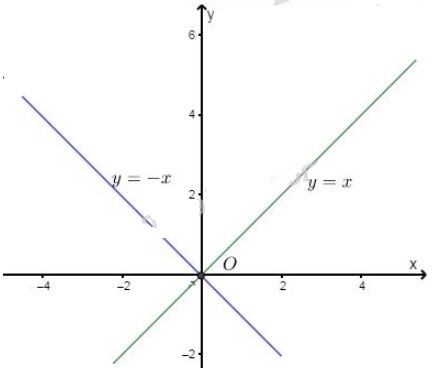
Bài 6 trang 11 SGK Toán lớp 9 tập 2 Câu hỏi: Đố: Bạn Nga nhận xét: Hai hệ phương trình bậc nhất hai ẩn vô nghiệm thì luôn tương đương với nhau. Bạn Phương khẳng định: Hai hệ phương trình bậc nhất hai ẩn cùng có vô số nghiệm thì cũng luôn tương đương với nhau. Theo em, các ý kiến đó đúng hay sai ? Vì sao ? (có thể cho một ví dụ hoặc minh họa bằng đồ thị). Lời giải: Bạn Nga đã nhận xét đúng vì hai hệ phương trình cùng vô nghiệm có nghĩa là chúng cùng có tập nghiệm bằng \(S=\phi \) (rỗng). Bạn Phương nhân xét sai. Chẳng hạn, hai hệ phương trình: \((I)\) \(\left\{\begin{matrix} y = x & & \\ y = x & & \end{matrix}\right.\) và \((II)\) \(\left\{\begin{matrix} y = -x & & \\ y = -x & & \end{matrix}\right.\)
Hệ (I) và hệ (II) đều có vô số nghiệm nhưng tập nghiệm của hệ \((I)\) được biểu diễn bởi đường thẳng \(y = x\), còn tập nghiệm của phương trình \((II)\) được biểu diễn bởi đường thẳng \(y = -x\). Hai đường thẳng này là khác nhau nên hai hệ đang xét không tương đương (vì không có cùng tập nghiệm). Sachbaitap.com
Xem thêm tại đây:
Bài 2. Hệ hai phương trình bậc nhất hai ẩn
|
-

Bài 7, 8, 9, 10, 11 trang 12 SGK Toán 9 tập 2 - Luyện tập
Giải bài 7, 8, 9, 10, 11 trang 12 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Luyện tập Hệ hai phương trình bậc nhất hai ẩn. Bài 11 Nếu tìm thấy hai nghiệm phân biệt của một hệ hai phương trình bậc nhất hai ẩn .
-

Bài 12, 13, 14 trang 15 SGK Toán 9 tập 2 - Giải hệ phương trình bằng phương pháp thế
Giải bài 12, 13, 14 trang 15 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Giải hệ phương trình bằng phương pháp thế. Bài 12 Giải các hệ phương trình sau bằng phương pháp thế
-

Bài 15, 16, 17, 18, 19 trang 15, 16 SGK Toán 9 tập 2 - Luyện tập
Giải bài 15 trang 15; bài 16, 17, 18, 19 trang 16 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Luyện tập - Giải hệ phương trình bằng phương pháp thế. Bài 19 Biết rằng: Đa thức P(x) chia hết cho đa thức x – a khi và chỉ khi P(a) = 0. Hãy tìm các giá trị của m và n sao cho đa thức sau đồng thời chia hết cho x + 1 và x – 3

 Tải ngay
Tải ngay