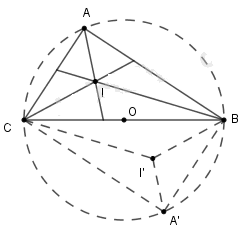
Bài 44, 45, 46, 47 trang 86 SGK Toán 9 tập 2 - Cung chứa góc

Bài 44 trang 86 SGK Toán lớp 9 tập 2

Câu hỏi:

Cho tam giác ABC vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm I khi A thay đổi.

Lời giải:

* Dự đoán : Quỹ tích điểm I là cung chứa góc 135º dựng trên đoạn BC.

* Chứng minh :

Phần thuận : 

Điểm A luôn nhìn đoạn thẳng AB dưới một góc \(90^\circ \) nên quỹ tích điểm \(A\) là đường tròn đường kính \(BC.\)

Xét tam giác \(ABC\) vuông tại \(A\) nên \(\widehat {ACB} + \widehat {ABC} = 90^\circ \), lại có \(BI\) là phân giác góc \(B\) và \(CI\) là phân giác góc \(C\) nên

\(\widehat {ICB} = \dfrac{1}{2}\widehat {ACB};\,\widehat {IBC} = \dfrac{1}{2}\widehat {ABC} \Rightarrow \widehat {ICB} + \widehat {IBC} = \dfrac{1}{2}\left( {\widehat {ACB} + \widehat {ABC}} \right) = \dfrac{1}{2}.90^\circ  = 45^\circ \)

Xét tam giác \(IBC\) có \(\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = 180^\circ  \Leftrightarrow \widehat {BIC} = 180^\circ  - 45^\circ  = 135^\circ \)

Nên số đo góc \(BIC\) luôn không đổi.

Vậy khi điểm A thay đổi trên đường tròn đường kính BC thì điểm I thay đổi và luôn nhìn đoạn thẳng BC dưới một góc \(135^\circ .\)

Vậy điểm I thuộc hai cung chứa góc \(135^\circ \) dựng trên đoạn BC.

Phần đảo: 

Chứng minh mọi điểm I thuộc cung chứa góc 135º dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện. 

+ Lấy I trên cung chứa góc 135º dựng trên đoạn BC

+ Kẻ tia Bx sao cho BI là phân giác của góc CBx

+ Kẻ tia Cy sao cho CI là phân giác của góc BCy

+ Bx cắt Cy tại A.

Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC

Ta có: 

\(\begin{array}{l}
\widehat {BAC} = {180^0} - \left( {\widehat B + \widehat C} \right)\\
= {180^0} - 2\left( {\widehat {IBC} + \widehat {ICB}} \right)\\
= {180^0} - 2\left( {{{180}^0} - \widehat {BIC}} \right)\\
= {180^0} - {360^0} + {2.135^0}\\
= {90^0}
\end{array}\)

Vậy ΔABC vuông tại A thỏa mãn đề bài. 

Kết luận: Quĩ tích các điểm I là hai cung chứa góc \(135^\circ \) dựng trên đoạn BC.

Bài 45 trang 86 SGK Toán lớp 9 tập 2

Câu hỏi:

Cho các hình thoi \(ABCD\) có cạnh \(AB\) cố định. Tìm quỹ tích giao điểm \(O\) của hai đường chéo của các hình thoi đó. 

Lời giải:

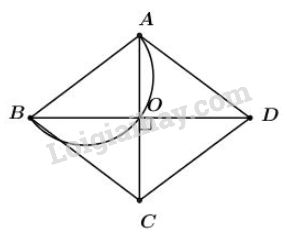
Dự đoán: Quỹ tích cần tìm là nửa đường tròn đường kính AB.

Chứng minh: 

Phần thuận:

Vì ABCD là hình thoi nên \(AC \bot BD\) tại \(O.\) (Tính chất)

Vậy điểm \(O\) nhìn \(AB\) cố định dưới góc \(90^0.\)

\(\Rightarrow \) Quỹ tích điểm \(O\) là nửa đường tròn đường kính \(AB.\)

Phần đảo: 

Chứng minh với mọi điểm O thuộc nửa đường tròn đường kính AB ta đều có hình thoi ABCD thỏa mãn đề bài.

+ Lấy điểm O thuộc nửa đường tròn đường kính AB

+ Lấy C đối xứng với A qua O

+ Lấy D đối xứng với B qua O.

Tứ giác ABCD có AC cắt BD tại O là trung điểm mỗi đường

⇒ ABCD là hình bình hành (Dấu hiệu nhận biết)

Mà O thuộc nửa đường tròn đường kính AB 

\(⇒ \widehat {AOB} = {90^0}\)

⇒ AC ⊥ DB

⇒ Hình bình hành ABCD là hình thoi (Hình bình hành có 2 đường chéo vuông góc)

Kết luận: Quỹ tích điểm O là nửa đường tròn đường kính AB (khác A và B)

Bài 46 trang 86 SGK Toán lớp 9 tập 2

Câu hỏi:

Dựng một cung chứa góc \(55^0\) trên đoạn thẳng \(AB = 3cm.\)

Phương pháp: 

Với đoạn thẳng \(AB\) và góc \(\alpha\, \, (0^0 < \alpha < 180^0)\) cho trước thì quỹ tích các điểm \(M\) thỏa mãn \(\widehat{AMB}=\alpha\) là hai cung chứa góc \(\alpha\) dựng trên đoạn \(AB.\)

Cách vẽ cung chứa góc \( \alpha\) dựng trên đoạn \(AB\).

+ Vẽ tia Ax tạo với AB một góc \( \alpha\)

+ Vẽ đường thẳng \( Ay \bot Ax\).

+ Vẽ đường trung trực d của đoạn thẳng AB. Gọi \( O\) là giao của \( Ay\) với \(d\).

+ Vẽ cung \(AmB\), tâm \(O\), bán kính \(OA\) sao cho cung này nằm ở nửa mặt phẳng bờ \(AB\) không chứa tia \(Ax\).

Cung \(AmB\) là một cung chứa góc \(\alpha\).

Lời giải:

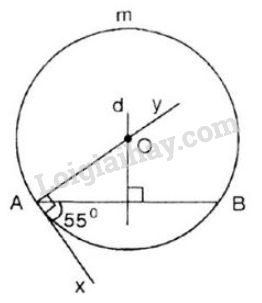
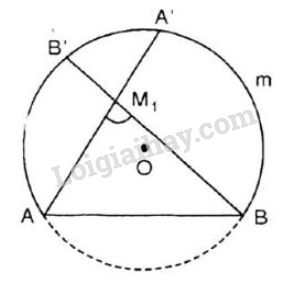
Cách dựng:

- Dựng đoạn thẳng \(AB = 3cm\) (dùng thước đo chia khoảng mm).

- Dựng góc \(\widehat{xAB} = 55^0\) (dùng thước đo góc và thước thẳng).

- Dựng tia \(Ay\) vuông góc với \(Ax\) (dùng êke).

- Dựng đường trung trực \(d\) của đoạn thẳng \(AB\) (dùng thước có chia khoảng và êke). Gọi \(O\) là giao điểm của \(d\) và \(Ay\).

- Dựng đường tròn tâm \(O,\) bán kính \(OA\) (dùng compa).

Ta có: \(\overparen{AmB}\) là cung chứa góc \(55^0\) dựng trên đoạn thẳng \(AB = 3cm\) (một cung).

Chứng minh:

+ O thuộc đường trung trực của AB

⇒ OA = OB

⇒ B thuộc đường tròn (O; OA).

Ax ⊥ AO ⇒ Ax là tiếp tuyến của (O; OA).

⇒ Góc BAx là góc tạo bởi tiếp tuyến Ax và dây AB

Lấy M ∈ cung AmB thì góc AMB là góc nội tiếp chắn cung nhỏ AB 

\( \Rightarrow \widehat {BAx} = \widehat {AMB}\)(Góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung)

\(\Rightarrow \widehat {AMB} = {55^0}\)

⇒ \(\overparen{AmB}\) là cung chứa góc 55º dựng trên đoạn AB = 3cm.

Kết luận: Bài toán có một nghiệm hình. 

Bài 47 trang 86 SGK Toán lớp 9 tập 2

Câu hỏi:

Gọi cung chứa góc \(55^0\) ở bài tập 46 là \(\overparen{AmB}\). Lấy điểm \({M_1}\) nằm bên trong và điểm \({M_2}\) nằm bên ngoài đường tròn chứa cung này sao cho \({M_1},{M_2}\) và cung \(\overparen{AmB}\) nằm cùng về một phía đối với đường thẳng \(AB\). Chứng minh rằng:

a) \(\widehat {A{M_1}B} > 55^0\);

b) \(\widehat {A{M_2}B} < 55^0\). 

Lời giải:

a) \({M_1}\) là điểm bất kì nằm trong cung chứa góc \(55^0\) (hình vẽ).

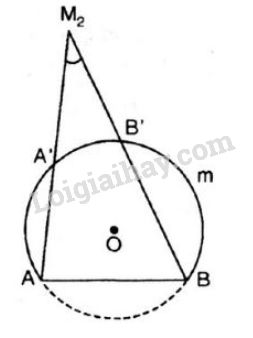
Gọi \(A', \,  B’\) theo thứ tự là giao điểm của \({M_1}A,\)  \({M_1}B\) với cung tròn.

Ta có \(\widehat {AA'B} = \dfrac{1}{2}\) sđ \(\overparen{AB} = 55^\circ \) (góc nội tiếp chắn cung \(AB\) và cung \(AmB\) là cung chứa góc \(55^\circ \))

Vì \(\widehat{A{M_1}B}\) là góc có đỉnh nằm trong đường tròn chắn cung \(A'B'\) và \(AB\) nên:  

\(\widehat {A{M_1}B}\) \(=\dfrac{sđ\overparen{AB}+sđ\overparen{A'B'}}{2}>\dfrac {1}{2}sđ\overparen{AB} =55^0\).

Vậy \(\widehat {A{M_1}B} > 55^0\) 

b)  \({M_2}\) là điểm bất kì nằm ngoài đường tròn (hình vẽ ) 

Ta có \({M_2}A, \, {M_2}B\) lần lượt cắt đường tròn tại \(A’, \, B’.\)

\(\widehat {AA'B} = \dfrac{1}{2}\) sđ \(AB = 55^\circ \) (góc nội tiếp chắn cung \(AB\) và cung \(AmB\) là cung chứa góc \(55^\circ \))

Vì góc \(\widehat {A{M_2}B}\) là góc có đỉnh nằm bên ngoài đường tròn chắn cung \(A'B'\) và \(AB\) nên:

\(\widehat {A{M_2}B}= \dfrac{sđ\overparen{AB}-sđ\overparen{A'B'}}{2}<\dfrac {1}{2}sđ\overparen{AB} =55^0 .\)

Vậy  \(\widehat {A{M_2}B} < 55^0.\)

Sachbaitap.com