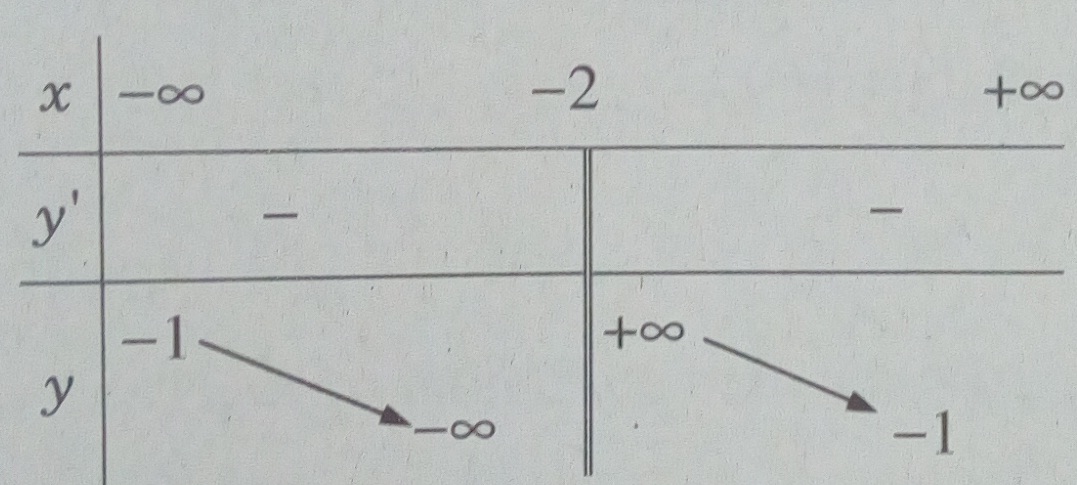
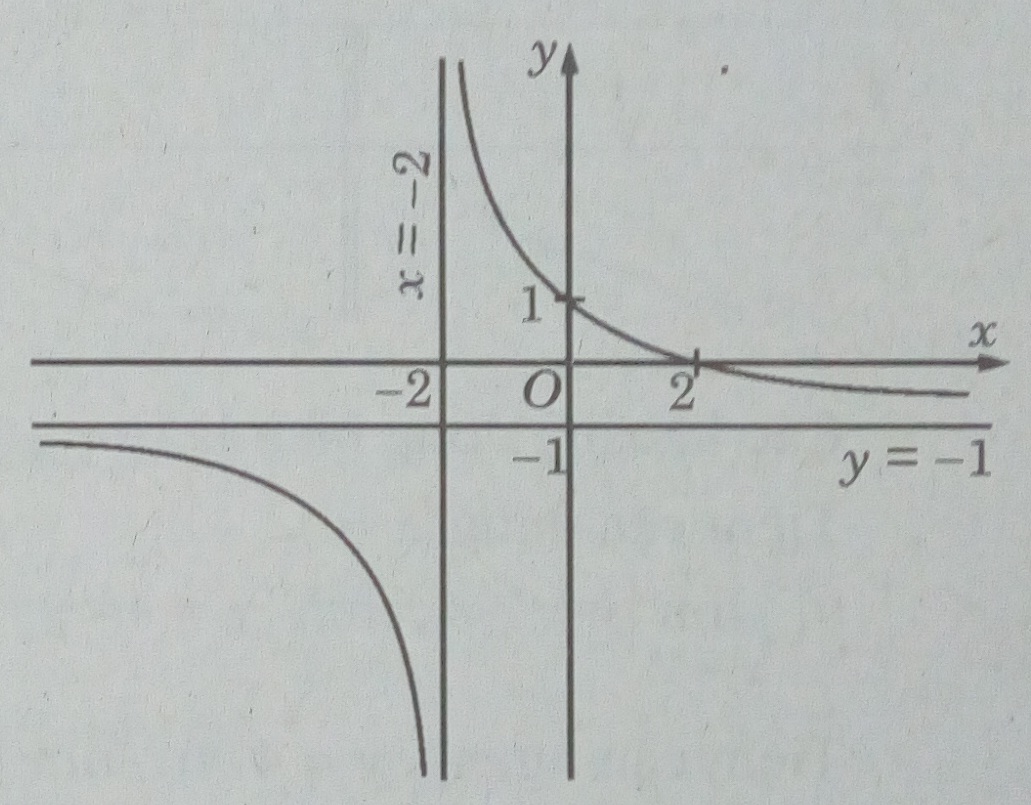
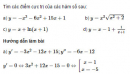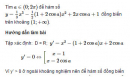Bài 5.2 trang 219 sách bài tập (SBT) - Giải tích 12a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: b) Viết phương trình tiếp tuyến của (C) , biết nó vuông góc với đường thẳng a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: \(y = {{ - x + 2} \over {x + 2}}\) b) Viết phương trình tiếp tuyến của (C) , biết nó vuông góc với đường thẳng \(y = {1 \over 4}x - 42\) Hướng dẫn làm bài a) \(y = {{ - x + 2} \over {x + 2}}\) +) Tập xác định: D = R\{-2} +) Ta có: \(y' = - {4 \over {{{(x + 2)}^2}}}\) Bảng biến thiên: Hàm số nghịch biến trên các khoảng \(( - \infty ; - 2),( - 2; + \infty )\) +) Tiệm cận đứng x = -2 vì \(\mathop {\lim }\limits_{x \to - {2^ + }} y = + \infty ,\mathop {\lim }\limits_{x \to - {2^ - }} y = - \infty \) Tiệm cận ngang y = -1 vì \(\mathop {\lim }\limits_{x \to \pm \infty } y = - 1\) Giao với các trục tọa độ: (0; 1); (2; 0) Đồ thị b) Tiếp tuyến của đồ thị có hệ số góc k = -4 (vì vuông góc với đường thẳng \(y = {1 \over 4}x - 42\) ) Hoành độ tiếp điểm thỏa mãn phương trình: \({{ - 4} \over {{{(x + 2)}^2}}} = - 4 = > \left[ {\matrix{{{x_1} = - 3} \cr {{x_2} = - 1} \cr} } \right.\) Ứng với \({x_1} = - 3\) ,ta có tiếp tuyến y = - 4x – 17 Ứng với \({x_2} = - 1\), ta có tiếp tuyến y = - 4x – 1. Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
BÀI TẬP ÔN TẬP CUỐI NĂM - GIẢI TÍCH 12
|
-
Bài 5.3 trang 219 sách bài tập (SBT) - Giải tích 12
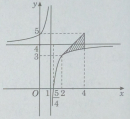
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số : b)Tính diện tích hình phẳng giới hạn bởi (C), tiếp tuyến của (C) tại A(2; 3) và đường thẳng x = 4.
-
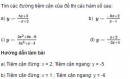
Bài 5.4 trang 219 sách bài tập (SBT) - Giải tích 12
Tìm các đường tiệm cận của đồ thị các hàm số sau:

 Tải ngay
Tải ngay