Bài 58, 59, 69, 61 trang 99 SGK Toán 8 tập 1 - Hình chữ nhậtBài 58, 59, 69, 61 trang 99 SGK Toán 8 tập 1 - Hình chữ nhật. Bài 61 Cho tam giác (ABC), đường cao (AH). Gọi (I) là trung điểm của (AC, E) là điểm đối xứng với (H) qua (I). Tứ giác (AHCE) là hình gì ? Vì sao ? Bài 58 trang 99 SGK Toán lớp 8 tập 1 Câu hỏi: Điền vào chỗ trống, biết rằng \(a, b\) là độ dài các cạnh, \(d\) là độ dài đường chéo của một hình chữ nhật.
Phương pháp: Áp dụng định lý Pytago. Lời giải:
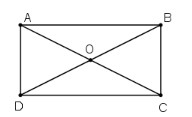
Bài 59 trang 99 SGK Toán lớp 8 tập 1 Câu hỏi: Chứng minh rằng: a. Giao điểm hai đường chéo của hình chữ nhật là tâm đối xứng của hình chữ nhật đó. b. Hai đường thẳng đi qua trung điểm hai cặp cạnh đối của hình chữ nhật là hai trục đối xứng của hình chữ nhật đó. Phương pháp: a. Áp dụng: +) Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó. +) Định nghĩa: Điểm \(O\) gọi là tâm đối xứng qua hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua điểm \(O\) cũng thuộc hình \(H.\) b. Áp dụng: Hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng. Hình chữ nhật cũng là 1 hình thang cân. Lời giải: a. Giả sử ABCD là hình chữ nhật. Gọi O là giao điểm của AC và BD. Theo tính chất đường chéo của hình chữ nhật ta có; hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường. Vậy: OA = OC và OB= OD Do đó, O là tâm đối xứng của hình chữ nhật đó.
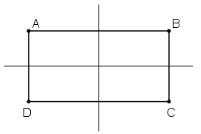
b. Áp dung tính chất: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó. ABCD là hình chữ nhật ⇒ ABCD là hình thang cân (hai đáy AB và CD) ⇒ Đường thẳng đi qua trung điểm AB và CD là trục đối xứng ABCD. Tương tự vậy: ABCD cũng là hình thang cân với hai đáy AD và BC ⇒ Đường thẳng đi qua trung điểm AD và BC là trục đối xứng của ABCD. Vậy ta có điều phải chứng minh.
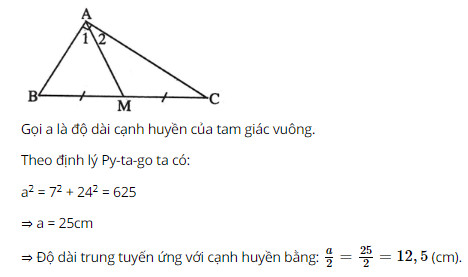
Bài 60 trang 99 SGK Toán lớp 8 tập 1 Câu hỏi: Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có các cạnh góc vuông bằng \(7cm\) và \(24cm\). Phương pháp: Áp dụng: +) Định lí Pytago. +) Tính chất: Trong tam giác vuông, trung tuyến ứng với cạnh huyền có độ dài bằng nửa độ dài cạnh ấy. Lời giải:
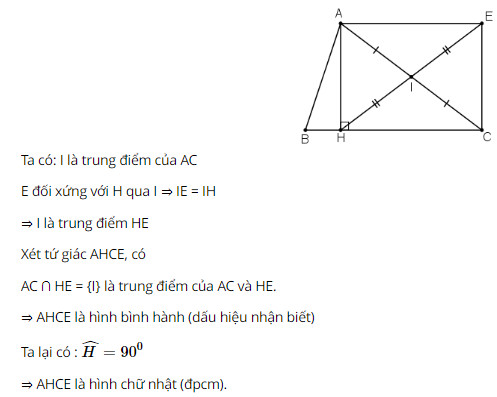
Bài 61 trang 99 SGK Toán lớp 8 tập 1 Câu hỏi: Cho tam giác \(ABC\), đường cao \(AH\). Gọi \(I\) là trung điểm của \(AC, E\) là điểm đối xứng với \(H\) qua \(I\). Tứ giác \(AHCE\) là hình gì ? Vì sao ? Phương pháp: Áp dụng dấu hiệu nhận biết hình bình hành: Tứ giác có 2 đường chéo cắt nhau tại trung điểm của mỗi đường Áp dụng dấu hiệu nhận biết hình chữ nhật: Hình bình hành có một góc vuông là hình chữ nhật. Lời giải:
Sachbaitap.com
Xem thêm tại đây:
Chương I. Tứ giác
|
-
Bài 62, 63, 64, 65, 66 trang 99, 100 SGK Toán 8 tập 1 - Luyện tập
Bài 62 trang 99,bài 63, 64, 65, 66 trang 100 SGK Toán 8 tập 1 - Luyện tập. Bài 65 Tứ giác (ABCD) có hai đường chéo vuông góc với nhau. Gọi (E, F, G, H) theo thứ tự là trung điểm của các cạnh (AB, BC, CD, DA). Tứ giác (EFGH) là hình gì? Vì sao?
-
Bài 67, 68, 69 trang 102, 103 SGK Toán 8 tập 1 - Đường thẳng song song với một đường thẳng cho trước
Bài 67, 68 trang 102, bài 69 trang 103 SGK Toán 8 tập 1 - Đường thẳng song song với một đường thẳng cho trước. Bài 68 Cho điểm (A) nằm ngoài đường thẳng (d) và có khoảng cách đến (d) bằng (2cm). Lấy điểm (B) bất kì thuộc đường thẳng (d). Gọi (C) là điểm đối xứng với điểm (A) qua điểm (B).
-

Bài 70, 71, 72 trang 102, 103 SGK Toán 8 tập 1 - Luyện tập
Bài 70, 71, 72 trang 102, 103 SGK Toán 8 tập 1 - Luyện tập. Bài 70 Cho góc vuông (xOy), điểm (A) thuộc tia (Oy) sao cho (OA = 2cm). Lấy (B) là một điểm bất kì thuộc tia (Ox). Gọi (C) là trung điểm của (AB). Khi điểm (B) di chuyển trên tia (Ox) thì điểm (C) di chuyển trên đường nào ?
-

Bài 73, 74, 75, 76, 77, 78 trang 105, 106 SGK Toán 8 tập 1 - Hình thoi
Bài 73, 74, 75, 76, 77, 78 trang 105, 106 SGK Toán 8 tập 1 - Hình thoi. Bài 77 Chứng minh rằng: a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi. b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi.

 Tải ngay
Tải ngay