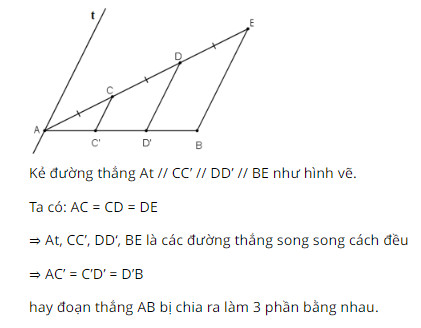
Bài 67, 68, 69 trang 102, 103 SGK Toán 8 tập 1 - Đường thẳng song song với một đường thẳng cho trước

Bài 67 trang 102 SGK Toán lớp 8 tập 1

Câu hỏi:

 Cho đoạn thẳng \(AB\). Kẻ tia \(Ax\) bất kì. Trên tia \(Ax\) lấy các điểm \(C, D, E\) sao cho \(AC = CD = DE\) (h.97). Kẻ đoạn thẳng \(EB\). Qua \(C, D\) kẻ các đường thẳng song song với \(EB\). Chứng minh rằng đoạn thẳng \(AB\) bị chia ra ba phần bằng nhau.

Phương pháp:

Áp dụng định lí:

- Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.

- Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.

Lời giải:

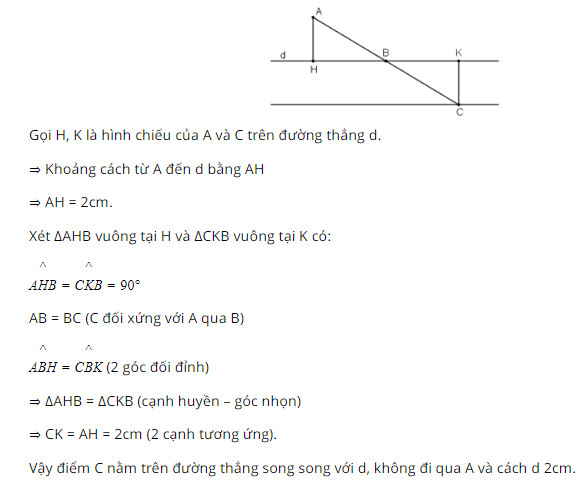
Bài 68 trang 102 SGK Toán lớp 8 tập 1

Câu hỏi:

Cho điểm \(A\) nằm ngoài đường thẳng \(d\) và có khoảng cách đến \(d\) bằng \(2cm\). Lấy điểm \(B\) bất kì thuộc đường thẳng \(d\). Gọi \(C\) là điểm đối xứng với điểm \(A\) qua điểm \(B\). Khi điểm \(B\) di chuyển trên đường thẳng \(d\) thì điểm \(C\) di chuyển trên đường nào ?

Phương pháp:

Áp dụng:

+) Hai điểm \(A\) và \(A'\) gọi là đối xứng nhau qua điểm \(O\) nếu \(O\) là trung điểm của \(AA'.\)

+) Tính chất: Các điểm cách đường thẳng \(b\) một khoảng bằng \(h\) nằm trên hai đường thẳng song song với \(b\) và cách \(b\) một khoảng bằng \(h.\)

Lời giải:

Bài 69 trang 103 SGK Toán lớp 8 tập 1

Câu hỏi:

Ghép mỗi ý (1), (2), (3), (4) với một trong các ý (5), (6), (7), (8) để được một khẳng định đúng:

(1) Tập hợp các điểm cách điểm \(A\) cố định một khoảng \(3cm\)

(2) Tập hợp các điểm cách đều hai đầu của đoạn thẳng \(AB\) cố định

(3) Tập hợp các điểm nằm trong góc \(xOy\) và cách đều hai cạnh của góc đó

(4) Tập hợp các điểm cách đều đường thẳng \(a\) cố định một khoảng \(3cm\)

(5) là đường trung trực của đoạn thẳng \(AB\).

(6) là hai đường thẳng song song với \(a\) và cách \(a\) một khoảng \(3cm\)

(7) là đường tròn tâm \(A\) bán kính \(3cm\).

(8) là tia phân giác của góc \(xOy\).

Phương pháp:

Áp dụng:

+ Đường tròn là tập hợp các điểm các đều một điểm cố định một khoảng cho trước.

+ Các điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

+ Tính chất một điểm thuộc tia phân giác của một góc thì cách đều \(2\) cạnh của góc đó.

+ Tập hợp các điểm cách một đường thẳng \(a\) cố định một khoảng bằng \(h\) không đổi là hai đường thẳng song song với \(a\) và cách \(a\) một khoảng bằng \(h.\)

Lời giải:

Ghép các ý:

    (1) với (7)

    (2) với (5)

    (3) với (8)

    (4) với (6)

Sachbaitap.com