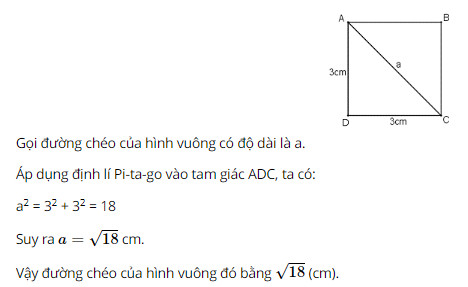
Bài 79, 80, 81, 82 trang 108 SGK Toán 8 tập 1 - Hình vuông

Bài 79 trang 108 SGK Toán lớp 8 tập 1

Câu hỏi:

a. Một hình vuông có cạnh bằng \(3cm\). Đường chéo của hình vuông đó bằng \(6cm\),  \(\sqrt{18}cm\), \(5cm\) hay \(4cm\) ?

b. Đường chéo của một hình vuông bằng \(2dm\). Cạnh của hình vuông đó bằng: \(1dm, \dfrac{3}{2}dm\), \(\sqrt{2}dm\) hay \(\dfrac{4}{3}dm\) ?

Phương pháp:

Áp dụng định lí Pytago: Bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

Lời giải:

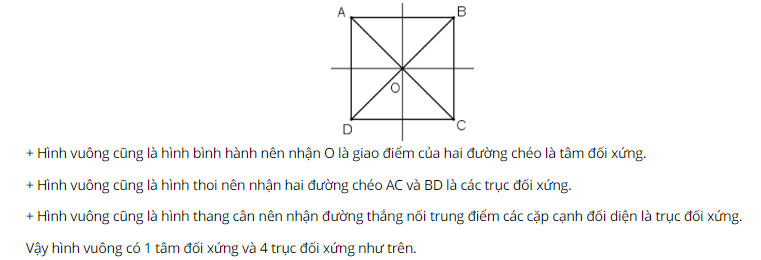
Bài 80 trang 108 SGK Toán lớp 8 tập 1

Câu hỏi:

Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông.

Phương pháp:

Áp dụng:  

+ Hình bình hành nhận giao điểm của hai đường chéo là tâm đối xứng.

+ Hình thang cân nhận đường thẳng nối trung điểm hai cạnh đáy là trục đối xứng.

+ Hình thoi nhận hai đường chéo là hai trục đối xứng. 

Lời giải:

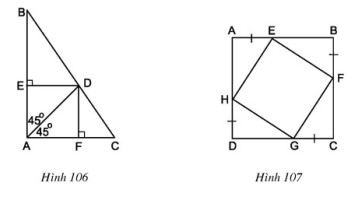
Bài 81 trang 108 SGK Toán lớp 8 tập 1

Câu hỏi:

Cho hình \(106.\) Tứ giác \(AEDF\) là hình gì ? Vì sao ? 

Phương pháp:

Áp dụng dấu hiệu nhận biết hình vuông: Hình thoi có một góc vuông là hình vuông.

Lời giải:

Cách 1:

Tứ giác AEDF có EA // DF (cùng vuông góc AF)

DE // FA (cùng vuông góc AE)

⇒ AEDF là hình bình hành (theo định nghĩa)

Hình bình hành AEDF có đường chéo AD là phân giác của góc A

⇒AEDF là hình thoi.

Hình thoi AEDF có Â = 90º

⇒ AEDF là hình vuông.

Cách 2:

Bài 82 trang 108 SGK Toán lớp 8 tập 1

Câu hỏi:

Cho hình \(107\), trong đó \(ABCD\) là hình vuông. Chứng minh rằng tứ giác \(EFGH\) là hình vuông. 

Phương pháp:

Áp dụng:

+) Dấu hiệu nhận biết hình thoi: Tứ giác có \(4\) cạnh bằng nhau là hình thoi.

+) Dấu hiệu nhận biết hình vuông: Hình thoi có một góc vuông là hình vuông.

Lời giải:

Do ABCD là hình vuông nên AB = BC = CD = DA.

Ta có: EB = AB – AE, CF = BC – BF, DG = DC – CG, AH = AD – DH 

Mà AE = BF = CG = DH (gt) và AB = BC = CD = DA (cmt)

$\Rightarrow$ BE = CF = DG = HA

Sachbaitap.com