Tải ngay
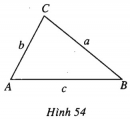
Bài 58 trang 48 SBT Hình học 10 Nâng caoGiải bài tập Bài 58 trang 48 SBT Hình học 10 Nâng cao Chứng minh rằng trong tam giác \(ABC\) ta có \(\cot A + \cot B + \cot C = \dfrac{{{a^2} + {b^2} + {c^2}}}{{abc}}R\). Giải \(\cot A = \dfrac{{\cos A}}{{\sin A}} = \dfrac{{\dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}}}{{\dfrac{a}{{2R}}}}\) \(= \dfrac{{{b^2} + {c^2} - {a^2}}}{{abc}}R\) Tương tự ta cũng có \(\cot B = \dfrac{{{a^2} + {c^2} - {b^2}}}{{abc}}R ;\) \( \cot C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{abc}}R.\) Từ đó suy ra \(\cot A + \cot B + \cot C = \dfrac{{{a^2} + {b^2} + {c^2}}}{{abc}}R.\) Sachbaitap.com
Xem thêm tại đây:
Bài 3. Hệ thức lượng trong tam giác.
|
