Bài 59 trang 48 SBT Hình học 10 Nâng caoGiải bài tập Bài 59 trang 48 SBT Hình học 10 Nâng cao a) \({b^2} - {c^2} = a(b\cos C - c\cos B).\) b) \(({b^2} - {c^2})\cos A = a(c\cos C - b\cos B)\). c) \(\sin C = \sin A\cos B + \sin B\cos A\). Giải
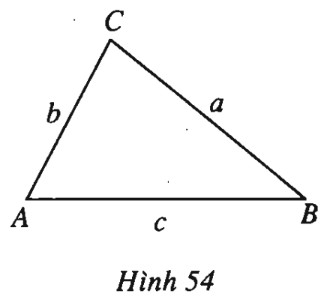
a) Ta có \(\begin{array}{l}{b^2} - {c^2} = ({a^2} + {c^2} - 2ac.\cos B) - ({a^2} + {b^2} - 2ab.\cos C)\\= {c^2} - {b^2} + 2a(b\cos C - c\cos B).\end{array}\) Từ đó ta được \(2({b^2} - {c^2}) = 2a(b\cos C - c\cos B)\), suy ra \({b^2} - {c^2} = a(b\cos C - c\cos B).\) b) \(\begin{array}{l}a(c\cos C - b\cos B) = ac\dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}} - ab\dfrac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\= \dfrac{1}{{2bc}}\left[ {{c^2}({a^2} + {b^2} - {c^2}) - {b^2}({a^2} + {c^2} - {b^2})} \right]\\= \dfrac{1}{{2bc}}\left[ {{a^2}({c^2} - {b^2}) + ({b^2} - {c^2})({b^2} + {c^2})} \right]\\= ({b^2} - {c^2})\dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = ({b^2} - {c^2})\cos A.\end{array}\) c) Đẳng thức cần chứng minh tương đương với đẳng thức \(2R\sin C = 2R\sin A\cos B + 2R\sin B\cos A\) hay \(c = a\cos B + b\cos A\). (h.54). Ta có \({\overrightarrow {AB} ^2} = \overrightarrow {AB} \left( {\overrightarrow {AC} + \overrightarrow {CB} } \right)\) \(= \overrightarrow {AB} .\overrightarrow {AC} + \overrightarrow {BA} .\overrightarrow {BC}. \) Suy ra \({c^2} = bc.\cos A + ac.\cos B\) dẫn đến \(c = b.\cos A + a.\cos B\) Sachbaitap.com
Xem thêm tại đây:
Bài 3. Hệ thức lượng trong tam giác.
|

 Tải ngay
Tải ngay