Bài 74 trang 49 SBT Hình học 10 Nâng caoGiải bài tập Bài 74 trang 49 SBT Hình học 10 Nâng cao Cho tam giác \(ABC\). Gọi \(r_a\) là bán kính đường tròn bàng tiếp góc \(A\). Chứng minh rằng diện tích tam giác \(ABC\) tính được theo công thức: \(S = (p - a){r_a}\). Giải
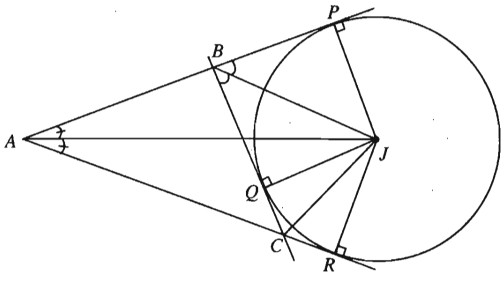
Gọi \(Q, R, P\) là các tiếp điểm của đường tròn bàng tiếp \((J ; r_a)\) lần lượt với các đường thẳng \(BC, CA, AB\) (h.67) thì: \(\begin{array}{l}{S_{JAB}} = \dfrac{1}{2}.AB.JP = \dfrac{{c.{r_a}}}{2} , \\{S_{JAC}} = \dfrac{1}{2}.AC.JR = \dfrac{{b.{r_a}}}{2} ,\\{S_{JBC}} = \dfrac{1}{2}.BC.JQ = \dfrac{{a{r_a}}}{2}.\end{array}\) Ta có \(S = {S_{JAB}} + {S_{JAC}} + {S_{JBC}}\) \(= \dfrac{{b + c - a}}{2}{r_a} = \dfrac{{a + b + c - 2a}}{2}{r_a}\). Vậy \(S = (p - a){r_a}\). Sachbaitap.com
Xem thêm tại đây:
Bài 3. Hệ thức lượng trong tam giác.
|

 Tải ngay
Tải ngay