Tải ngay
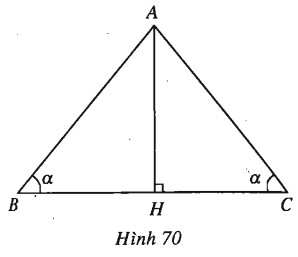
Bài 84 trang 51 SBT Hình học 10 Nâng caoGiải bài tập Bài 84 trang 51 SBT Hình học 10 Nâng cao Cho tam giác cân có góc ở đáy bằng \(\alpha \). Chứng minh rằng \(2\sin \alpha \cos \alpha = \sin 2\alpha \). Giải (h.70).
Xét tam giác \(ABC\) cân ở đỉnh \(A\) có góc đáy bằng \(\alpha \), \(AH\) là đường cao. Ta có \(\begin{array}{l}S = \dfrac{1}{2}AH.BC = AH.BH\\S = \dfrac{1}{2}.AB.AC.\sin ({180^0} - 2\alpha ) \\= \dfrac{1}{2}.AB.AC.\sin 2\alpha \end{array}\) Từ đó suy ra \(2AH.BH = AB.AC.\sin 2\alpha\) \( \Rightarrow \sin 2\alpha = 2.\dfrac{{BH}}{{AB}}.\dfrac{{AH}}{{AC}}\) \(= 2\cos \alpha .\sin \alpha \) Sachbaitap.com
Xem thêm tại đây:
Bài tập Ôn tập chương II - Tích vô hướng của hai vectơ và ứng dụng
|
