Tải ngay
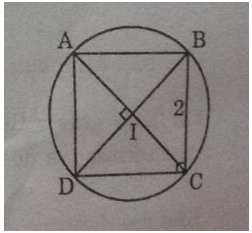
Câu 11 trang 158 Sách Bài Tập (SBT) Toán 9 Tập 1Cho hình vuông ABCD. Câu 11 trang 158 Sách Bài Tập (SBT) Toán 9 Tập 1. a) Chứng minh rằng bốn đỉnh của hình vuông cùng nằm trên một đường tròn. Hãy chỉ ra vị trí của tâm đường tròn đó. b) Tính bán kính của đường tròn đó, biết cạnh của hình vuông bằng 2dm. Gợi ý làm bài
a) Gọi I là giao điểm của hai đường chéo AC và BD Ta có: IA = IB = IC = ID (tính chất của hình vuông) Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn. Tâm của đường tròn là I. b) Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có: \(A{C^2} = A{B^2} + B{C^2} = {2^2} + {2^2} = 8\) Suy ra: \(AC = \,2\sqrt 2 \,(dm)\) Vậy \(R = IA = {{AC} \over 2} = {{2\sqrt 2 } \over 2} = \sqrt 2 \,(dm)\) Sachbaitap.com
Xem lời giải SGK - Toán 9 - Xem ngay >> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn
|
-
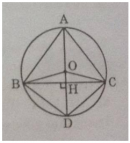
Câu 12 trang 158 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho tam giác ABC cân tại A, nội tiếp đường tròn (O).
-
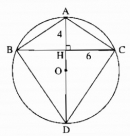
Câu13* trang 158 Sách bài tập (SBT) Toán 9 Tập 1
Tam giác ABC cân tại A, BC = 12cm, đường cao AH = 4cm. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.
-
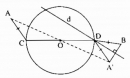
Câu 14* trang 158 Sách bài tập (SBT) Toán 9 Tập 1
Cho đường tròn (O) và hai điểm A, B nằm bên ngoài đường tròn. Dựng đường kính COD sao cho AC = BD.
-
Câu 1.1 trang 158 Sách bài tập (SBT) Toán lớp 9 Tập 1
Xét tính đúng – sai của mỗi khẳng định sau: Cho tam giác ABC nội tiếp đường tròn (O).
