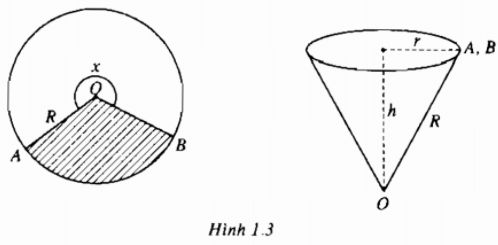
Câu 1.26 trang 14 sách bài tập Giải tích 12 Nâng caoCắt bỏ hình quạt AOB (hình phẳng có nét gạch trong hình 1.3) từ một mảnh các tông hình tròn bán kính R Cắt bỏ hình quạt AOB (hình phẳng có nét gạch trong hình 1.3) từ một mảnh các tông hình tròn bán kính R rồi dán hai bán kính OA và OB của một hình quạt còn lại với nhau để được một cái phễu có dạng một hình nón. Gọi x là góc ở tâm của hình quạt tròn dùng làm phễu (h.1.3), \(0 < x < 2\pi \) a) Hãy biểu diễn hán kính r của hình tròn đáy và đường cao h của hình nón theo R và x. b) Tính thể tích hình nón theo R và x. c) Tìm x để hình nón có thể tích lớn nhất và tính giá trị lớn nhất đó.
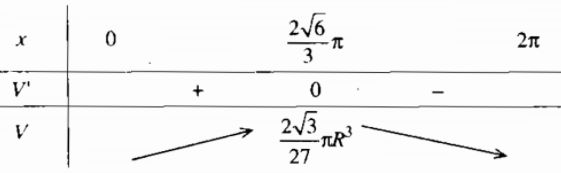
Giải a) Vì độ dài của đường tròn đáy hình nón bằng độ dài \(\overparen{AB}\) của quạt tròn dùng làm phễu, nên ta có \(2\pi r = Rx\) Do đó \(r = {{Rx} \over {2\pi }}\) và \(h = \sqrt {{R^2} - {r^2}} = \sqrt {{R^2} - {{{R^2}{x^2}} \over {4{\pi ^2}}}} = {R \over {2\pi }}\sqrt {4{\pi ^2} - {x^2}} \) b) Thể tích hình nón là \(V = {1 \over 3}\pi {r^2}h = {{{R^3}} \over {24{\pi ^2}}}{x^2}\sqrt {4{\pi ^2} - {x^2}} ,0 < x < 2\pi \) c) Ta tìm \(x \in \left( {0;2\pi } \right)\) sao cho tại đó V đạt giá trị lớn nhất \(V' = {{{R^3}} \over {24{\pi ^2}}}.{{x\left( {8{\pi ^2} - 3{x^2}} \right)} \over {\sqrt {4{\pi ^2} - {x^2}} }}\) Với \(0 < x < 2\pi \), ta có \(V' = 0 \Leftrightarrow 8{\pi ^2} - 3{x^2} = 0 \Leftrightarrow x = {{2\sqrt 6 } \over 3}\pi \approx 1,63\pi \) Hình nón có thể tích lớn nhất khi \(x = {{2\sqrt 6\pi } \over 3} \approx 1,63\pi \) \(\mathop {\max }\limits_{x \in \left( {0;2\pi } \right)} V = V({{2\sqrt 6 \pi} \over 3}) = {{2\sqrt 3 } \over {27}}\pi {R^3}\) Sacbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 3. Giá trị lớn nhất và nhỏ nhất của hàm số
|
-
Câu 1.29 trang 16 sách bài tập Giải tích 12 Nâng cao
Lưu lượng xe ô tô vào đường hầm được cho bởi công thức
-

Câu 1.30 trang 16 sách bài tập Giải tích 12 Nâng cao
Một ngọn hải đăng đặt tại vị trí A cách bờ biển một khoảng AB = 5km
-

Câu 1.32 trang 16 sách bài tập Giải tích 12 Nâng cao
Cũng câu hỏi như trong bài tập 1.31 đối cới các hàm số sau:

 Tải ngay
Tải ngay