Câu 134 trang 97 Sách bài tập (SBT) Toán 8 tập 1Chứng minh rằng trong hình thoi: a. Giao điểm của hai đường chéo là tâm đối xứng của hình thoi b. Hai đường chéo là hai trục đối xứng của hình thoi. Chứng minh rằng trong hình thoi: a. Giao điểm của hai đường chéo là tâm đối xứng của hình thoi b. Hai đường chéo là hai trục đối xứng của hình thoi. Giải:
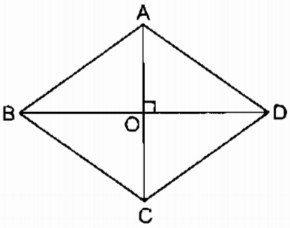
a. Hình bình hành có tâm đối xứng là giao điểm của hai đường chéo. Hình thoi cũng là một hình bình hành nên cũng có tâm đối xứng là giao điểm hai đường chéo của nó. b. Ta có: AC ⊥ BD (tính chất hình thoi) OB = OD ( tính chất hình thoi) nên AC là đường trung trực của BD. Do đó điểm đối xứng với điểm B qua AC là điểm D Điểm đối xứng với điểm A qua AC là điểm A Điểm đối xứng với điểm C qua AC là điểm C Vậy điểm đối xứng với mỗi đỉnh của hình thoi qua AC cũng thuộc hình thoi. Do đó AC là trục đối xứng của hình thoi ABCD. OC = OA ( tính chất hình thoi) nên BD là đường trung trực của AC Do đó điểm đối xứng với điểm A qua BD là điểm C Điểm đối xứng với điểm B qua BD là điểm B Điểm đối xứng với điểm D qua BD là điểm D Vậy điểm đối xứng với mỗi đỉnh của hình thoi qua BD cũng thuộc hình thoi. Do đó BD là trục đối xứng của hình thoi ABCD. Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 11. Hình thoi
|
-
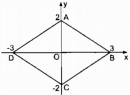
Câu 135 trang 97 Sách bài tập (SBT) Toán 8 tập 1
Tứ giác ABCD có tọa độ các đỉnh như sau: A(0; 2), B( 3; 0), C(0; −2 ), D(−3; 0). Tứ giác ABCD là hình gì ? Tính chu vi của tứ giác đó ?
-
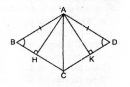
Câu 136 trang 97 Sách bài tập (SBT) Toán 8 tập 1
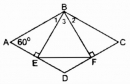
a. Cho hình thoi ABCD. Kẻ hai đường cao AH, AK. Chứng minh rằng AH = AK b. Hình bình hành ABCD có hai đường cao AH , AK bằng nhau. Chứng minh rằng ABCD là hình thoi.

 Tải ngay
Tải ngay