Tải ngay
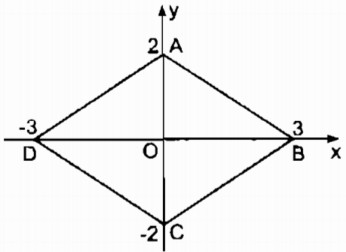
Câu 135 trang 97 Sách bài tập (SBT) Toán 8 tập 1Tứ giác ABCD có tọa độ các đỉnh như sau: A(0; 2), B( 3; 0), C(0; −2 ), D(−3; 0). Tứ giác ABCD là hình gì ? Tính chu vi của tứ giác đó ? Tứ giác ABCD có tọa độ các đỉnh như sau: A(0; 2), B( 3; 0), C(0; −2 ), D(−3; 0). Tứ giác ABCD là hình gì ? Tính chu vi của tứ giác đó ? Giải:
A(0; 2) và C(0; −2) nên hai điểm A và C đối xứng nhau qua O (0, 0) ⇒ OA = OC B(3; 0) và D(−3; 0) nên hai điểm B và D đối xứng qua O (0; 0) ⇒ OB = OD Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường) Ox ⊥ Oy hay AC ⊥ BD Vậy tứ giác ABCD là hình thoi Trong ∆ OAB vuông tại O. Theo định lý Pi-ta-go ta có: \(\eqalign{ & A{B^2} = O{A^2} + O{B^2} \cr & A{B^2} = {2^2} + {3^2} = 4 + 9 = 13 \cr & AB = \sqrt {13} \cr} \) Chu vi hình thoi bằng \(4\sqrt {13} \) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 11. Hình thoi
|
-
Câu 136 trang 97 Sách bài tập (SBT) Toán 8 tập 1
a. Cho hình thoi ABCD. Kẻ hai đường cao AH, AK. Chứng minh rằng AH = AK b. Hình bình hành ABCD có hai đường cao AH , AK bằng nhau. Chứng minh rằng ABCD là hình thoi.
