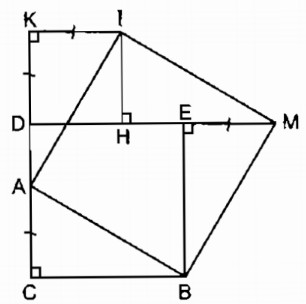
Câu 152 trang 99 Sách bài tập (SBT) Toán 8 tập 1Chứng minh rằng ABMI là hình vuông. Cho hình vuông DEBC. Trên cạnh CD lấy điểm A, trên tia đối của tia DC lấy điểm K, trên tia đối tia ED lấy điểm M sao cho CA = DK = EM. Vẽ hình vuông DKIH (H thuộc cạnh DE). Chứng minh rằng ABMI là hình vuông. Giải:
Xét ∆ CAB và ∆ EMB : CA = ME (gt) \(\widehat C = \widehat E = {90^0}\) CB = EB (tính chất hình vuông) Do đó: ∆ CAB = ∆ EMB (c.g.c) ⇒ AB = MB (1) AK = DK +DA CD = CA + AD mà CA = DK nên AK = CD Xét ∆ CAB và ∆ KIA : CA = KI (vì cùng bằng DK) \(\widehat C = \widehat K = {90^0}\) CB = AK (vì cùng bằng CD) Do đó: ∆ CAB = ∆ KIA (c.g.c) ⇒ AB = AI (2) DH = DK (vì KDHI là hình vuông) EM = DK (gt) ⇒ DH + HE = HE + EM hay DE = HM Xét ∆ HIM và ∆ EMB : HI = EM (vì cùng bằng DK) \(\widehat H = \widehat E = {90^0}\) HM = EB (vì cùng bằng DE) Do đó: ∆ HIM = ∆ EMB (c.g.c) ⇒ IM = MB (3) Từ (1), (2) và (3) suy ra: AB = BM = AI = IM Tứ giác ABMI là hình thoi. Mặt khác, ta có ∆ ACB = ∆ MEB (chứng minh trên) \(\eqalign{ & \Rightarrow \widehat {CBA} = \widehat {EBM} \cr & \widehat {CBA} + \widehat {ABE} = \widehat {CBE} = {90^0} \cr} \) Suy ra: \(\widehat {EBM} + \widehat {ABE} = {90^0}\) hay \(\widehat {ABM} = {90^0}\) Vậy : Tứ giác ABMI là hình vuông. Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 12. Hình vuông
|
-
Câu 153 trang 99 Sách bài tập (SBT) Toán 8 tập 1
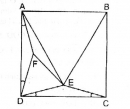
Cho tam giác ABC. Vẽ ở ngoài tam giác các hình vuông ABDE, ACFH. a. Chứng minh rằng EC = BH, EC ⊥ BH.
-
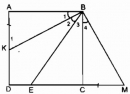
Câu 154 trang 99 Sách bài tập (SBT) Toán 8 tập 1
Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD ở K. Chứng minh rằng AK + CE = BE.
-
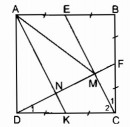
Câu 155 trang 99 Sách bài tập (SBT) Toán 8 tập 1
Cho hình vuông ABCD. Gọi E, F theo thứ tự là trung điểm của AB, BC. a. Chứng minh rằng CE vuông góc với DF

 Tải ngay
Tải ngay