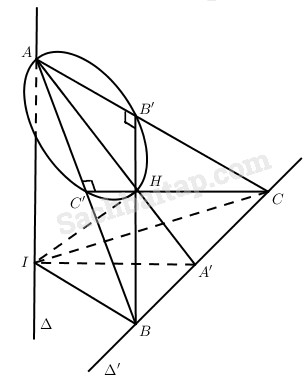
Câu 16 trang 223 Sách bài tập Hình học 11 Nâng cao

Cho hai đường thẳng ∆ và ∆’ chéo nhau và vuông góc với nhau. (P) là mặt phẳng chứa đường thẳng ∆’ và vuông góc với ∆ (A ≠ I). Hai điểm B, C thay đổi trên ∆’ sao cho mp(B, ∆) vuông góc với mp(C, ∆). Gọi AA’, BB’, CC’ là các đường cao của tam giác ABC. Chứng minh rằng:

a) \(A{B^2} + A{C^2} - B{C^2}\) không đổi.

b) A’B.A’C không đổi và trực tâm của tam giác ABC là điểm cố định.

c) Các điểm B’, C’ thuộc một đường tròn cố định.

Trả lời

Ta có \(AI \bot \left( {IBC} \right)\) nên \(\widehat {BIC}\) hoặc \({180^0} - \widehat {BIC}\) là góc giữa mp(B, ∆) và mp(C, ∆).

Theo giả thiết \(mp\left( {B,\Delta } \right) \bot mp\left( {C,\Delta } \right)\) nên \(\widehat {BIC} = {90^0}\). Như vậy tứ diện IABC có IA, IB, IC đôi một vuông góc.

a) Ta có

Quảng cáo

\(\eqalign{  & A{B^2} + A{C^2} - B{C^2}  \cr  &  = A{I^2} + I{B^2} + A{I^2} + I{C^2} - B{C^2}  \cr  &  = 2{\rm{A}}{I^2} \cr} \)

Điều này khẳng định \(A{B^2} + A{C^2} - B{C^2}\) không đổi.

b) Dễ thấy IA’ là đường cao của tam giác vuông IBC. Vậy \(A'B.A'C = IA{'^2}\).

Vì \(IA' \bot \Delta '\) nên IA’ là cố định, do đó A’B.A’C không đổi.

Vì IABC là tứ diện có các cạnh IA, IB, IC đôi một vuông góc nên trực tâm của tam giác ABC là hình chiếu H của điểm I trên mặt phẳng (ABC) (trùng với mặt phẳng (A, ∆’)). Vậy trực tâm H của tam giác ABC là điểm cố định.

c) Ta có B’, C’ thuộc mp(A, ∆).

\(\widehat {AB'H} = \widehat {AC'H} = {90^0}\).

Vậy B’, C’ thuộc đường tròn đường kính AH trong mp(A, ∆’). Đường tròn này cố định.

Sachbaitap.com