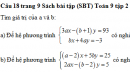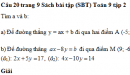Giải các hệ phương trình:
\(a)\left\{ {\matrix{
{1,7x - 2y = 3,8} \cr
{2,1x + 5y = 0,4} \cr} } \right.\)
\(b)\left\{ {\matrix{
{\left( {\sqrt 5 + 2} \right)x + y = 3 - \sqrt 5 } \cr
{ - x + 2y = 6 - 2\sqrt 5 } \cr} } \right.\)
Giải
a)
\(\eqalign{
& \left\{ {\matrix{
{1,7x - 2y = 3,8} \cr
{2,1x + 5y = 0,4} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{17x - 20y = 38} \cr
{21x + 50y = 4} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = {{17x - 38} \over {20}}} \cr
{21x + 50.{{17x - 38} \over {20}} = 4} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = {{17x - 38} \over {20}}} \cr
{42x + 85x - 190 = 8} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = {{17x - 38} \over {20}}} \cr
{127x = 198} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = {{17x - 38} \over {20}}} \cr
{x = {{198} \over {127}}} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = - {{73} \over {127}}} \cr
{x = {{198} \over {127}}} \cr} } \right. \cr} \)
Vậy hệ phương trình có 1 nghiệm duy nhất: \((x; y) = \left( {{{198} \over {127}}; - {{73} \over {127}}} \right)\)
b)
\(\eqalign{
& \left\{ {\matrix{
{\left( {\sqrt 5 + 2} \right)x + y = 3 - \sqrt 5 } \cr
{ - x + 2y = 6 - 2\sqrt 5 } \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = 3 - \sqrt 5 - \left( {\sqrt 5 + 2} \right)x} \cr
{ - x + 2\left[ {3 - \sqrt 5 - \left( {\sqrt 5 + 2} \right)x} \right] = 6 - 2\sqrt 5 } \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = 3 - \sqrt 5 - \left( {\sqrt 5 + 2} \right)x} \cr
{ - x + 6 - 2\sqrt 5 - \left( {2\sqrt 5 + 4} \right)x = 6 - 2\sqrt 5 } \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = 3 - \sqrt 5 - \left( {\sqrt 5 + 2} \right)x} \cr
{ - x\left( {2\sqrt 5 + 5} \right) = 0} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = 3 - \sqrt 5 - \left( {\sqrt 5 + 2} \right)x} \cr
{x = 0} \cr} } \right.\cr& \Leftrightarrow \left\{ {\matrix{
{y = 3 - \sqrt 5 } \cr
{x = 0} \cr} } \right. \cr} \)
Vậy hệ phương trình có 1 nghiệm duy nhất: \((x; y) = \left( {0;3 - \sqrt 5 } \right)\).
Sachbaitap.com

 Tải ngay
Tải ngay