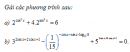Câu 2.105 trang 87 sách bài tập Giải tích 12 Nâng caoCho a >1, b >1.Chứng minh rằng, nếu phương trình a) Cho a >1, b >1.Chứng minh rằng, nếu phương trình \({a^x} + {b^x} = c\) có nghiệm \({x_0}\) thì nhiệm đó là duy nhất. b) Chứng minh kết quả tương tự với trường hợp 0< a < 1 và 0 Giải a) Khi a >1, b >1 thì các hàm số \(y = {a^x}\), \(y = {b^x}\) đồng biến. Với \(x > {x_0}\) ta có \({a^x} > {a^{{x_0}}};{b^x} > {b^{{x_0}}}\). Vì vậy \({a^x} + {b^x} > {a^{{x_0}}} + {b^{{x_0}}} = c\) Với \(x < {x_0}\) ta có \({a^x} < {a^{{x_0}}};{b^x} < {b^{{x_0}}}\). Vì vậy \({a^x} + {b^x} < {a^{{x_0}}} + {b^{{x_0}}} = c\) Do đó phương trình \({a^x} + {b^x} = c\) có nghiệm \({x_0}\) thì nghiệm đó là duy nhất. b) Cách giải tương tự như câu a), với lưu ý khi \(0 < a < 1,0 < b < 1\) thì các hàm số \(y = {a^x},y = {b^x}\)nghịch biến. Câu a) và b) được minh họa bởi các ví dụ sau: \({4^x} + {6^x} = {13.2^x} \Leftrightarrow {2^x} + {3^x} = 13\) có nghiệm duy nhất \(x = 2\) \({16^x} + {9^x} = {25^x} \Leftrightarrow {\left( {{{16} \over {25}}} \right)^x} + {\left( {{9 \over {25}}} \right)^x} = 1\) có nghiệm duy nhất \(x = 1\) Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 7. Phương trình mũ và lôgarit
|
-
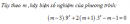
Câu 2.109 trang 88 sách bài tập Giải tích 12 Nâng cao
Tùy theo m ,hãy biện số nghiệm của phương trình:

 Tải ngay
Tải ngay