Câu 2.106 trang 87 sách bài tập Giải tích 12 Nâng caoGiải các phương trình sau: Giải các phương trình sau: a) \({2^{{{\cos }^2}x}} + {4.2^{{{\sin }^2}x}} = 6\) b) \({3^{2\sin x + 2\cos x + 1}} - {\left( {{1 \over {15}}} \right)^{ - \cos x - \sin x{\rm{ - lo}}{{\rm{g}}_{15}}8}} \) \(+ {5^{^{2\sin x + 2\cos x + 1}}} = 0.\) Giải a) Đặt \(t = {2^{{\rm{co}}{{\rm{s}}^2}x}}\left( {1 \le t \le 2} \right)\), ta được phương trình \({t^2} - 6t + 8 = 0\). Giải ra ta được \(t = 4\) (loại) và \(t = 2\) Với \(t=2\) ta có: \({2^{{{\cos }^2}x}} = 2 \Leftrightarrow {\cos ^2}x = 1 \) \(\Leftrightarrow \sin x = 0 \Leftrightarrow x = k\pi (k \in Z)\) b) \(x = {{3\pi } \over 4} + k\pi ;x = \pi + k2\pi \left( {k \in Z} \right)\) Biến đổi phương trình về dạng \({3.3^{2\left( {\sin x + \cos x} \right)}} - {8.15^{\cos x + \sin x}} + {5.5^{2\left( {\sin x + \cos x} \right)}} = 0.\) Chia cả hai vế của phương trình cho \({3^{2\left( {\sin x + \cos x} \right)}}\), rồi đặt \(t = {\left( {{5 \over 3}} \right)^{{\rm{cos}}x + {\mathop{\rm s}\nolimits} {\rm{in}}x}}\) với \(\left( {t > 0} \right)\) dẫn đến phương trình: \(5{t^2} - 8t + 3 = 0\) Giải ra ta được \(t = 1\) và \(t = {3 \over 5}\) - Với \(t = 1\) ta có \({\left( {{5 \over 3}} \right)^{{\rm{cos}}x + {\mathop{\rm s}\nolimits} {\rm{in}}x}} = 1\), dẫn đến \({\rm{cos}}x + \sin x = 0\) hay \({\rm{cos}}\left( {x - {\pi \over 4}} \right) = 0\) Do vậy \(x = {{3\pi } \over 4} + k\pi \left( {k \in Z} \right)\) - Với \(t = {3 \over 5}\) ta có \({\left( {{5 \over 3}} \right)^{{\rm{cos}}x + {\mathop{\rm s}\nolimits} {\rm{in}}x}} = {3 \over 5}\), dẫn đến \({\rm{cos}}x + \sin x = - 1\) hay \({\rm{cos}}\left( {x - {\pi \over 4}} \right) = - {1 \over {\sqrt 2 }}\) Do vậy \(x = \pi + k2\pi ;x = {-\pi \over 2} + k2\pi \left( {k \in Z} \right)\) Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 7. Phương trình mũ và lôgarit
|
-
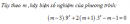
Câu 2.109 trang 88 sách bài tập Giải tích 12 Nâng cao
Tùy theo m ,hãy biện số nghiệm của phương trình:

 Tải ngay
Tải ngay










