Câu 2.24 trang 64 sách bài tập Đại số và Giải tích 11 Nâng caoCho 5 chữ số 0,1, 3, 6, 9 có thể lập được a) Bao nhiêu số tự nhiên có 4 chữ số khác nhau b) Bao nhiêu số lẻ với 4 chữ số khác nhau c) Bao nhiêu số chẵn có 4 chữ số khác nhau d) Bao nhiêu số tự nhiên có 4 chữ số khác nhau và chia hết cho 3. Cho 5 chữ số 0,1, 3, 6, 9 có thể lập được a) Bao nhiêu số tự nhiên có 4 chữ số khác nhau b) Bao nhiêu số lẻ với 4 chữ số khác nhau c) Bao nhiêu số chẵn có 4 chữ số khác nhau d) Bao nhiêu số tự nhiên có 4 chữ số khác nhau và chia hết cho 3. Giải a) Có\(A_5^4 = 120\) số có 4 chữ số khác nhau từ tập các chữ số \(\left\{ {0,1,3,6,9} \right\}\) (có thể bắt đầu với chữ số 0). Có \(A_4^3 = 24\) số có 4 chữ số bắt đầu bởi số 0. Vậy có \(120 - 24 = 96\) số có 4 chữ số khác nhau. b) Xét việc lập số lẻ \(\overline {abcd} \). Chữ số \(d \in \left\{ {1,3,9} \right\}\) có 3 cách chọn. Chữ số a có \(4 - 1 = 3\) cách chọn. Chữ số b có \(5 - 2 = 3\) cách chọn và chữ số c có 2 cách chọn. Vậy có 3.3.3.2 = 54 số lẻ. c) Có \(96 - 54 = 42\) số chẵn. d) Một số chia hết cho 3 khi và chỉ khi tổng các chữ số của nó chia hết cho 3. Trong tập hợp \(\left\{ {0,1,3,6,9} \right\}\) có duy nhất số 1 chia hết cho 3. Vậy số đó chia hết cho 3 khi và chỉ khi các chữ số của nó thuộc tập \(\left\{ {0,3,6,9} \right\}\). Có 4! Số có 4 chữ số khác nhau từ \(\left\{ {0,3,6,9} \right\}\) (có thể bắt đầu với chữ số 0). Có 3! Số có 4 chữ số khác nhau từ \(\left\{ {0,3,6,9} \right\}\) bắt đầu với chữ số 0. Vậy kết quả là có \(4! - 3! = 24 - 6 = 18\) số. sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 2: Hoán vị, chỉnh hợp và tổ hợp
|
-

Câu 2.25 trang 64 sách bài tập Đại số và Giải tích 11 Nâng cao
Trong một đa giác lồi n cạnh (n > 3) ta kẻ tất cả các đường chéo. Biết rằng không có ba đường chéo nào trong chúng đồng quy. TÌm số giao điểm của các đường chéo này.
-

Câu 2.26 trang 64 sách bài tập Đại số và Giải tích 11 Nâng cao
Trong mặt phẳng cho đa giác đều H có 20 cạnh. Hỏi a) Có bao nhiêu tam giác mà cả ba đỉnh đều là đỉnh của H? b) Trong số các tam giác ở câu a) có bao nhiêu tam giác mà i) Có đúng hai cạnh là cạnh của H? ii) Có đúng một cạnh là cạnh của H? iii) Không có cạnh nào là cạnh của H?
-

Câu 2.27 trang 64 sách bài tập Đại số và Giải tích 11 Nâng cao
Cho hai đường thẳng a, b song song. Xét tập H có 30 điểm khác nhau, trong đó trên đường thẳng a có 10 điểm và trên đường thẳng b có 20 điểm của H. Có bao nhiêu tam giác mà các đỉnh của nó thuộc tập H?
-
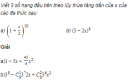
Câu 2.28 trang 65 sách bài tập Đại số và Giải tích 11 Nâng cao
Viết 3 số hạng đầu tiên theo lũy thừa tăng dần của x của các đa thức sau:

 Tải ngay
Tải ngay







