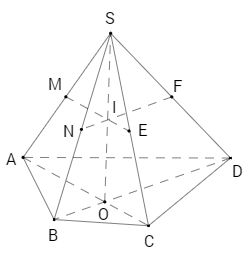
Câu 25 trang 55 Sách bài tập Hình học 11 nâng cao.Cho hình chóp tứ giác S.ABCD có đáy là một tứ giác lồi. Gọi M, N, E, F lần lượt là trung điểm của cạnh bên SA, SB, SC và SD. 25. Trang 55 Sách bài tập Hình học 11 nâng cao. Cho hình chóp tứ giác S.ABCD có đáy là một tứ giác lồi. Gọi M, N, E, F lần lượt là trung điểm của cạnh bên SA, SB, SC và SD. Chứng minh rằng: a) ME//AC, NF//BD. b) Ba đường thẳng ME, NF và SO (O là giao điểm của AC và BD) đồng quy. c) Bốn điểm M, N, E, F đồng phẳng. Giải
a) Xét tam gác SAC. Ta có ME là đường trung bình nên ME//AC. Lí luận tương tự, NF//BD. b) Trong mp(SAC) gọi I là giao điểm của ME và SO. Dễ thấy I là trung điểm của SO. Từ đó FI là đường trung bình của tam giác SOD. Vậy FI//DO. Gọi N’ là giao điểm của đường thẳng FI với SB. Do FN' // BD và F là trung điểm của SD suy ra N’ là trung điểm của SB, tức là \(N' \equiv N.\) Vậy ba đường thẳng ME, NF, SO đồng quy tại I. c) Do ME và NF cắt nhau tại I, nên qua ME và NF xác định một mặt phẳng. Từ đó suy ra bốn điểm M, N, E, F đồng phẳng. sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 2: Hai đường thẳng song song
|
-

Câu 26 trang 55 Sách bài tập Hình học 11 nâng cao.
Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật. Gọi M, N, E, F lần lượt là trọng tâm của các tam giác SAB, SCD và SDA.
-

Câu 27 trang 55 Sách bài tập Hình học 11 nâng cao.
Cho tứ diện ACBD. Gọi I và J lần lượt là trung điểm của BC và BD; E là một điểm thuộc cạnh AD khác với A và D.
-

Câu 28 trang 55 Sách bài tập Hình học 11 nâng cao.
Cho hình chóp S.ABCD có đáy là một tứ giác lồi. Gọi M và N lần lượt là trọng tâm của tam giác SAB và SAD; E là trung điểm của CB.

 Tải ngay
Tải ngay