Câu 2.74 trang 82 sách bài tập Giải tích 12 Nâng caoTính các giới hạn sau: Tính các giới hạn sau: a) \(\mathop {\lim }\limits_{x \to 9} {\log _3}x\) b) \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {4x + 1} \right)} \over x}\) c) \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {3x + 1} \right) - \ln \left( {2x + 1} \right)} \over x}\) d) \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {1 + 3x} \right)} \over {\sin 2x}}\) Hướng dẫn: d) Vận dụng công thức \(\mathop {\lim }\limits_{x \to 0} {{\sin x} \over x} = 1\) Giải a) \(\mathop {\lim }\limits_{x \to 9} {\log _3}x={\log _3}9 = 2\) b) \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {4x + 1} \right)} \over x}\) \(=\mathop {\lim }\limits_{x \to 0} 4.{{\ln \left( {4x + 1} \right)} \over {4x}}=4.1=4\) c) \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {3x + 1} \right) - \ln \left( {2x + 1} \right)} \over x} \) \(= \mathop {\lim }\limits_{x \to 0} {{\ln \left( {3x + 1} \right)} \over {3x}}.3 - \mathop {\lim }\limits_{x \to 0} {{\ln \left( {2x + 1} \right)} \over {2x}}.2 = 3 - 2 = 1\) d) \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {1 + 3x} \right)} \over {\sin 2x}} = \mathop {\lim }\limits_{x \to 0} {{{{\ln \left( {1 + 3x} \right)} \over {3x}}} \over {{{\sin 2x} \over {2x}}}}.{3 \over 2} = {{\mathop {\lim }\limits_{x \to 0} {{\ln \left( {1 + 3x} \right)} \over {3x}}} \over {\mathop {\lim }\limits_{x \to 0} {{\sin 2x} \over {2x}}}}.{3 \over 2} = {3 \over 2}\) Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 5, 6. Hàm số mũ , hàm số lôgarit và hàm số lũy thừa
|
-
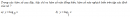
Câu 2.77 trang 82 sách bài tập Giải tích 12 Nâng cao
Trong các hàm số sau đây, hãy chỉ ra hàm số nào đồng biến, hàm số nào nghịch biến trên tập xác định của nó ?
-

Câu 2.79 trang 83 sách bài tập Giải tích 12 Nâng cao
Tính giá trị gắn đúng của đạo hàm của mỗi hàm số sau tại điểm đã chỉ ra (chính xác đến hàng phần nghìn):

 Tải ngay
Tải ngay









