Tải ngay
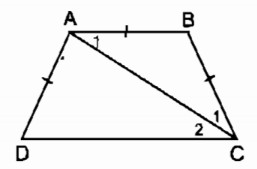
Câu 28 trang 83 Sách bài tập (SBT) Toán 8 tập 1Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng CA là tia phân giác của góc C. Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng CA là tia phân giác của góc C. Giải:
AB = AD (gt) AD = BC (tính chất hình thang cân) ⇒ AB = BC do đó ∆ ABC cân tại B \(\Rightarrow {\widehat A_1} = {\widehat C_1}\) (tính chất tam giác cân) Mặt khác: AB // CD (gt) \({\widehat A_1} = {\widehat C_2}\) (hai góc so le trong) Suy ra: \({\widehat C_1} = {\widehat C_2}\) Vậy CA là tia phân giác của \(\widehat {BCD}\). Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 3. Hình thang cân
|
-
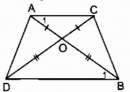
Câu 29 trang 83 Sách bài tập (SBT) Toán 8 tập 1
Hai đoạn thẳng AB và CD cắt nhau tại O. Biết rằng OA = OC, OB = OD. Tứ giác ACBD là hình gì ? Vì sao ?
-
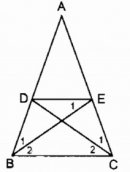
Câu 30 trang 83 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE.
-
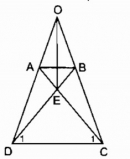
Câu 31 trang 83 Sách bài tập (SBT) Toán 8 tập 1
Hình thang cân ABCD có O là giao điểm của hai đường thẳng chứa cạnh bên AD, BC và E là giao điểm của hai đường chéo. Chứng minh rằng OE là đường trung trực của hai đáy.
-
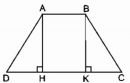
Câu 32 trang 83 Sách bài tập (SBT) Toán 8 tập 1
a.Hình thang cân ABCD có đáy nhỏ AB = b, đáy lớn CD = a, đường cao AH.
