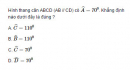-
Câu 22 trang 82 Sách bài tập (SBT) Toán 8 tập 1
Hình thang cân ABCD có AB// CD, AB < CD. Kẻ các đường cao AH, BK. Chứng minh rằng DH = CK.
-
Câu 23 trang 82 Sách bài tập (SBT) Toán 8 tập 1
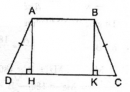
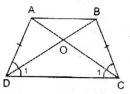
Hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo. Chứng minh rằng OA=OB, OC=OD.
-
Câu 24 trang 83 Sách bài tập (SBT) Toán 8 tập 1
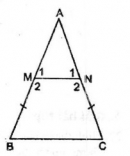
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN.
-
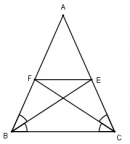
Câu 25 trang 83 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.
-
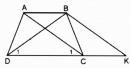
Câu 26 trang 83 Sách bài tập (SBT) Toán 8 tập 1
Chứng minh rằng hình thang có hai đường chéo bằng nhau là hình thang cân.
-

Câu 28 trang 83 Sách bài tập (SBT) Toán 8 tập 1
Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng CA là tia phân giác của góc C.
-
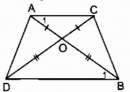
Câu 29 trang 83 Sách bài tập (SBT) Toán 8 tập 1
Hai đoạn thẳng AB và CD cắt nhau tại O. Biết rằng OA = OC, OB = OD. Tứ giác ACBD là hình gì ? Vì sao ?
-
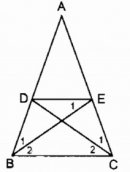
Câu 30 trang 83 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE.
-
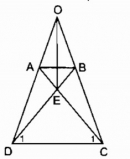
Câu 31 trang 83 Sách bài tập (SBT) Toán 8 tập 1
Hình thang cân ABCD có O là giao điểm của hai đường thẳng chứa cạnh bên AD, BC và E là giao điểm của hai đường chéo. Chứng minh rằng OE là đường trung trực của hai đáy.
-
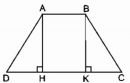
Câu 32 trang 83 Sách bài tập (SBT) Toán 8 tập 1
a.Hình thang cân ABCD có đáy nhỏ AB = b, đáy lớn CD = a, đường cao AH.
-
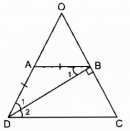
Câu 33 trang 83 Sách bài tập (SBT) Toán 8 tập 1
Hình thang cân ABCD có đường chéo DB vuông góc với cạnh bên BC, BD là tia phân giác của góc D. Tính chu vi của hình thang, biết BC = 3cm.
-
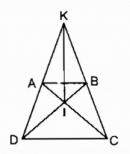
Câu 3.2 trang 84 Sách bài tập (SBT) Toán lớp 8 tập 1
Hình thang cân ABCD (AB// CD) có hai đường chéo cắt nhau tại I, hai đường thẳng chứa các cạnh bên cắt nhau ở K. Chứng minh rằng KI là đường trung trực của hai đáy.
-
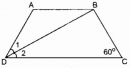
Câu 3.3 trang 84 Sách bài tập (SBT) Toán 8 tập 1
Tính các cạnh của hình thang, biết chu vi hình thang bằng 20cm.

 Tải ngay
Tải ngay