Tải ngay
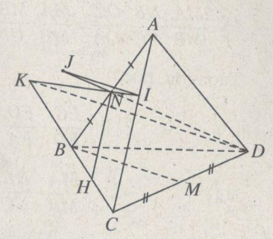
Câu 30 trang 55 Sách bài tập Hình học 11 nâng cao.Cho tứ diện đều ABCD có cạnh bằng a. Gọi M và N lần lượt là trung điểm của CD và AB. 30. Trang 55 Sách bài tập Hình học 11 nâng cao. Cho tứ diện đều ABCD có cạnh bằng a. Gọi M và N lần lượt là trung điểm của CD và AB. a) Hãy xác định điểm \(I \in AC,\,J \in DN\) sao cho IJ//BM. b) Tính độ dài đoạn thẳng IJ theo a. Giải a) Trong mp(BCD), từ D kẻ đường thẳng song song với BM cắt CB tại K. Đường thẳng KN cắt AC tại I. Trong mp(IKD), từ I kẻ đường thẳng song song với DK cắt đường thẳng DN tại J. Khi đó theo cách dựng ta có IJ // BM.
b) Do BM là đường trung bình của tam giác CKD nên \(KD = 2BM = 2.{{a\sqrt 3 } \over 2} = a\sqrt 3 \) Gọi H là trung điểm của BC. Khi đó: \(\eqalign{ Vậy \(IJ = {1 \over 3}KD = {{a\sqrt 3 } \over 3}\). sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 2: Hai đường thẳng song song
|
-
Câu 31 trang 56 Sách bài tập Hình học 11 nâng cao.
Cho tứ diện ABCD và bốn điểm M, N, E, F lần lượt nằm trên các cạnh AB, BC, CD và DA.
-
Câu 32 trang 56 Sách bài tập Hình học 11 nâng cao.
Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm của SC, N là trung điểm của OB (O là giao điểm của BD và AC).
-
Câu 33 trang 56 Sách bài tập Hình học 11 nâng cao.
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.
-
Câu 34 trang 57 Sách bài tập Hình học 11 nâng cao.
Cho tứ diện ABCD. Gọi M là trung điểm của AB và N là một điểm thuộc cạnh CD không trùng với C và D. Mặt phẳng (P) qua MN và song song với BC.
