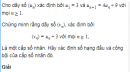Câu 3.43 trang 92 sách bài tập Đại số và Giải tích 11 Nâng caoCho cấp số cộng Cho cấp số cộng \(({u_n})\) có \({u_2} + {u_5} = 42\) và \({u_4} + {u_9} = 66\). Hãy tính tổng 346 số hạng đầu tiên của cấp số cộng đó. Giải Ta có \(\eqalign{ Từ đó, kí hiệu \({S_{346}}\) là tổng cần tính, ta được \({S_{346}} = {{346.(2{u_1} + 345d)} \over 2} = {{346.(2 \times 11 + 345 \times 4)} \over 2} = 242546\) sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 3. Cấp số cộng
|
-
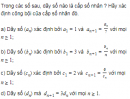
Câu 3.46 trang 92 sách bài tập Đại số và Giải tích 11 Nâng cao
Trong các số sau, dãy số nào là cấp số nhân ? Hãy xác định công bội của cấp số nhân đó.

 Tải ngay
Tải ngay