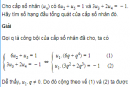Câu 3.50 trang 93 sách bài tập Đại số và Giải tích 11 Nâng caoMột cấp số nhân có 7 số hạng với số hạng đầu và cộng bội là số âm. Biết rằng tích của số hạng thứ ba và số hạng số hạng thứ năm bằng 6. Hãy tìm các số hạng còn lại của cấp số nhân đó. Một cấp số nhân có 7 số hạng với số hạng đầu và cộng bội là các số âm. Biết rằng tích của số hạng thứ ba và số hạng số hạng thứ năm bằng 5184, tích của số hạng thứ năm và số hạng cuối bằng 746496. Hãy tìm cấp số nhân đó. Giải Với mỗi \(n \in \left\{ {1,2,3,4,5,6,7} \right\},\) kí hiệu \({u_n}\) là số hạng thứ n của cấp số nhân cần tìm. Theo giả thiết ta có \({u_3}.{u_5} = 5184\) và \({u_5}.{u_7} = 746496\) Vì cấp số nhân đã cho có số hạng đầu và công bội là các số âm nên \({u_1} < 0,{u_2} > 0,{u_3} < 0,{u_4} > 0,\) \({u_5} < 0,{u_6} > 0,{u_7} < 0\) Từ đó \(\left. \matrix{ \(\Rightarrow u_5^2 = {u_4}.{u_6} = 72 \times 864 = 62208 \) \(\Rightarrow {u_5} = - 144\sqrt 3 \) Suy ra \({u_7} = {{746496} \over { - 144\sqrt 3 }} = - 1728\sqrt 3 \) \({u_3} = {{5184} \over { - 144\sqrt 3 }} = - 12\sqrt 3 \) \({u_2} = {{u_3^2} \over {{u_4}}} = {{432} \over {72}} = 6\) \({u_1} = {{u_2^2} \over {{u_3}}} = {{36} \over { - 12\sqrt 3 }} = - \sqrt 3 \) Vậy cấp số nhân cần tìm là: \( - \sqrt 3 ,6, - 12\sqrt 3 ,72, - 144\sqrt 3 ,864, - 1728\sqrt 3 \) sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 4. Cấp số nhân
|
-

Câu 3.51 trang 93 sách bài tập Đại số và Giải tích 11 Nâng cao
Tìm tam giác có ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC được gọi là tam giác trung bình của tam giác ABC.
-

Câu 3.52 trang 93 sách bài tập Đại số và Giải tích 11 Nâng cao
Cho một cấp số có 7 số hạng, số hạng thứ tư bằng 6 và số hạng thứ 7 gấp 243 lần số hạng thứ hai. Hãy tìm các số hạng còn lại của cấp số nhân đó.

 Tải ngay
Tải ngay