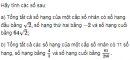
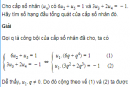Câu 3.52 trang 93 sách bài tập Đại số và Giải tích 11 Nâng cao

Cho một cấp số có 7 số hạng, số hạng thứ tư bằng 6 và số hạng thứ 7 gấp 243 lần số hạng thứ hai. Hãy tìm các số hạng còn lại của cấp số nhân đó.

Giải

Với  mỗi \(n \in \left\{ {1,2,3,4,5,6,7} \right\},\) kí hiệu \({u_n}\) là số hạng thứ n của cấp số nhân đã cho. Kí hiệu q là công bội của cấp số nhân đó.

Theo giả thiết ta có \({u_4} = 6,{u_7} = 243{u_2}\) và theo yêu cầu của bài ra ta cần tính \({u_1},{u_2},{u_3},{u_4},{u_5},{u_6},{u_7}.\)

Hiển nhiên có \({u_2} \ne 0\); vì nếu ngược lại thì phải có \({u_4} = 0\), trái với giả thiết của bài ra. Vì thế, từ giả thiết \({u_7} = 243{u_2}\), theo công thức xác định số hạng tổng quát của một cấp số nhân, ta được

                     \(243 = {{{u_7}} \over {{u_2}}} = {{{u_1}.{q^6}} \over {{u_1}.q}} = {q^5}.\) 

Suy ra \(q = 3.\) Vì thế, từ giả thiết \({u_4} = 6\) ta được \({u_1} = {{{u_4}} \over {{q^3}}} = {6 \over {{3^3}}} = {2 \over 9}.\)

Từ đó : \({u_2} = {u_1}.q = {2 \over 3},{u_3} = {u_2}.q = 2,{u_5} = {u_4}.q = 18,\)

\({u_6} = {u_5}.q = 54,{u_7} = {u_6}.q = 162.\)

sachbaitap.com