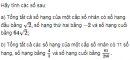
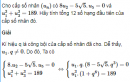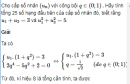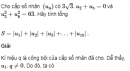Câu 3.55 trang 94 sách bài tập Đại số và Giải tích 11 Nâng caoCho cấp số nhân Cho cấp số nhân \(({u_n})\) và cho các số nguyên dương m, k với \(m < k.\) Chứng minh rằng \(\left| {{u_k}} \right| = \sqrt {{u_{k - m}}.{u_{k + m}}} .\) Áp dụng. Hãy tìm một cấp số nhân với công bội âm, có 7 số hạng, số hạng thứ hai bằng 2 và tích của số hạng đầu với số hạng cuối bằng 18. Giải Kí hiệu q là công bội của cấp số nhân \(({u_n})\). Xét hai trường hợp sau : \( - \) Trường hợp 1 : \(q = 0.\) Khi đó \({u_n} = 0\) với mọi \(n \ge 2.\) Vì thế, hiển nhiên ta có điều cần chứng minh. \( - \) Trường hợp 2 : \(q \ne 0.\) Khi đó \(\eqalign{ Từ đó suy ra \({u_{k - m}}.{u_{k + m}} = u_k^2\) hay \(\left| {{u_k}} \right| = \sqrt {{u_{k - m}}.{u_{k + m}}} \) Áp dụng. Với mỗi \(n \in \left\{ {1,2,3,4,5,6,7} \right\},\) kí hiệu \({u_n}\) là số hạng thứ n của cấp số nhân cấn tìm. Theo giả thiết của bài ra, ta có \({u_3} = 2\) và \({u_1}.{u_7} = 18.\) Vì cấp số nhân cần tìm có công bội âm và \({u_3} > 0\) nên \({u_4} < 0\). Do đó, áp dụng kết quả đã chứng minh ở trên cho \(m = 3\) và \(k = 4,\) ta được \({u_4} = - \sqrt {{u_1}.{u_7}} = - \sqrt {18} = - 3\sqrt 2 .\) Suy ra \(q = {{{u_4}} \over {{u_3}}} = - {{3\sqrt 2 } \over 2}.\) Do đó \(\eqalign{ Vậy, cấp số nhân cần tìm là : \({4 \over 9}, - {{2\sqrt 2 } \over 3},2, - 3\sqrt 2 ,9, - {{27\sqrt 2 } \over 2},{{81} \over 2}.\) sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 4. Cấp số nhân
|

 Tải ngay
Tải ngay