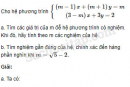Câu 3.57 trang 68 SBT Đại số 10 Nâng caoGiải bài tập Câu 3.57 trang 68 SBT Đại số 10 Nâng cao Giải và biện luận các phương trình theo tham số m : a. \(\dfrac{{\left( {2m - 1} \right)x + 2}}{{x - 2}} = m + 1\) b. \(\dfrac{{\left( {m - 1} \right)\left( {m + 2} \right)x}}{{2x + 1}} = m + 2\) Giải: a. Với điều kiện x ≠ 2, phương trình đã cho tương đương với phương trình \(\left( {m - 2} \right)x = - 2\left( {m + 2} \right)\) (1) Nếu m = 2 thì (1) vô nghiệm nên phương trình đã cho vô nghiệm. Nếu m ≠ 2 thì (1) có nghiệm duy nhất \(x = \dfrac{{ - 2\left( {m + 2} \right)}}{{m - 2}}.\) Để là nghiệm của phương trình đã cho, giá trị này phải thỏa mãn điều kiện x ≠ 2, tức là : \(\dfrac{{ - 2\left( {m + 2} \right)}}{{m - 2}} \ne 2\) Điều đó xảy ra khi và chỉ khi m ≠ 0. Vậy, ta có kết luận : • Nếu m = 2 hoặc m = 0 thì phương trình đã cho vô nghiệm. • Nếu m ≠ 2 và m ≠ 0 thì phương trình đã cho có nghiệm \(x = \dfrac{{ - 2\left( {m + 2} \right)}}{{m - 2}}\) b. Điều kiện là \(x \ne - \dfrac{1}{2}\) • Nếu m ≠ -2 , m ≠ 1 và m ≠ 3 thì phương trình có nghiệm \(x = \dfrac{1}{{m - 3}}\) . • Nếu m = -2 thì phương trình nghiệm đúng với mọi \(x \ne - \dfrac{1}{2}.\) • Nếu m = 1 hoặc m = 3 thì phương trình vô nghiệm. Sachbaitap.com
Xem thêm tại đây:
Bài tập Ôn tập chương III - Phương trình bậc nhất và bậc hai
|

 Tải ngay
Tải ngay