Tải ngay
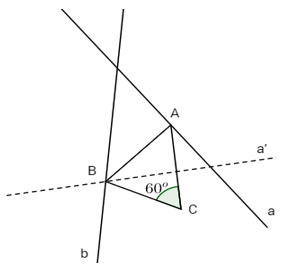
Câu 36 trang 10 Sách bài tập Hình Học 11 nâng cao.Cho hai đường thẳng a, b phân biệt và điểm C không nằm trên chúng. Hãy xác định hai điểm A, B lần lượt nằm trên a và b sao cho tam giác ABC là tam giác đều. 36. Trang 10 Sách bài tập Hình Học 11 nâng cao. Cho hai đường thẳng a, b phân biệt và điểm C không nằm trên chúng. Hãy xác định hai điểm A, B lần lượt nằm trên a và b sao cho tam giác ABC là tam giác đều. Giải Giả sử đã dựng tam giác đều ABC thỏa mãn điều kiện cho. Khi đó, góc \(\left( {CA,CB} \right) = \pm{60^o}.\) Nếu \(\left( {CA,CB} \right) = {60^o}\) thì phép quay Q tâm C góc quay \({60^o}\) sẽ biến A thành B và biến đường thẳng a thành đường thẳng a’ đi qua B. Vậy ta có thể xác định điểm B như sau:
Dựng đường thẳng a’ là ảnh của đường thẳng a qua phép quay Q, rồi lấy giao điểm B của a’ và b. Điểm A được xác định như là ảnh của B qua phép quay tâm C góc quay \( - {60^o}.\) Làm tương tự cho trường hợp \(\left( {CA,CB} \right) = - {60^o}.\) Bài toán có ít nhất một nghiệm hình, có thể có vô số nghiệm hình. sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> Học trực tuyến Lớp 11 cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng. Cam kết giúp học sinh lớp 11 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 4: Phép quay và phép đối xứng tâm
|
-
Câu 37 trang 11 Sách bài tập Hình Học 11 nâng cao.
Cho hình vuông ABCD và một điểm M nằm trên một cạnh của hình vuông. Tìm các điểm N, P nằm trên cạnh của hình vuông sao cho tam giác MNP là tam giác đều.
-
Câu 38 trang 11 Sách bài tập Hình Học 11 nâng cao.
Hãy kể ra các phép dời hình biến tam giác ABC thành chính nó.
-
Câu 40 trang 11 Sách bài tập Hình Học 11 nâng cao.
Cho tam giác đều ABC với (AB, AC) = (BC, BA) = (CA, CB).
