-

Câu 30 trang 10 Sách bài tập Hình Học 11 nâng cao.
Cho hai điểm A, B phân biệt. Chứng minh rằng nếu phép dời hình F biến A thành B và biến B thành A thì F là phép đối xứng trục hoặc phép đối xứng tâm.
-

Câu 31 trang 10 Sách bài tập Hình Học 11 nâng cao.
Chứng minh rằng hợp thành của một số phép quay với các tâm quay trùng nhau là một phép quay.
-

Câu 32 trang 10 Sách bài tập Hình Học 11 nâng cao.
Hợp thành của một số lẻ các phép đối xứng trục có các trục đối xứng đồng quy là một phép đối xứng trục.
-

Câu 33 trang 10 Sách bài tập Hình Học 11 nâng cao.
Cho đường tròn (O) và một điểm I không nằm trên đường tròn. Với mỗi điểm A thay đổi trên đường tròn, ta xét hình vuông ABCD có tâm I. Tìm quỹ tích các điểm B, C, D.
-

Câu 34 trang 10 Sách bài tập Hình Học 11 nâng cao.
Cho đường thẳng a và một điểm G không nằm trên a. Với mỗi điểm nằm trên a ta dựng tam giác đều ABC có tâm G. Tìm quỹ tích hai điểm B và C khi A chạy trên a.
-

Câu 36 trang 10 Sách bài tập Hình Học 11 nâng cao.
Cho hai đường thẳng a, b phân biệt và điểm C không nằm trên chúng. Hãy xác định hai điểm A, B lần lượt nằm trên a và b sao cho tam giác ABC là tam giác đều.
-

Câu 37 trang 11 Sách bài tập Hình Học 11 nâng cao.
Cho hình vuông ABCD và một điểm M nằm trên một cạnh của hình vuông. Tìm các điểm N, P nằm trên cạnh của hình vuông sao cho tam giác MNP là tam giác đều.
-

Câu 38 trang 11 Sách bài tập Hình Học 11 nâng cao.
Hãy kể ra các phép dời hình biến tam giác ABC thành chính nó.
-
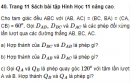
Câu 40 trang 11 Sách bài tập Hình Học 11 nâng cao.
Cho tam giác đều ABC với (AB, AC) = (BC, BA) = (CA, CB).
-

Câu 41 trang 11 Sách bài tập Hình Học 11 nâng cao.
Hãy chỉ ra tất cả các phép dời hình biến hình vuông ABCD thành chính nó.
-

Câu 42 trang 11 Sách bài tập Hình Học 11 nâng cao.
Hãy chứng tỏ rằng F và F’ là những phép đối xứng tâm và nêu rõ cách xác định tâm đối xứng của phép đó.
-

Câu 43 trang 11 Sách bài tập Hình Học 11 nâng cao.
Chứng minh rằng khi cố định hai điểm A, B và cho điểm C thay đổi thì đường thẳng NQ luôn luôn đi qua một điểm cố định.
-

Câu 44 trang 11 Sách bài tập Hình Học 11 nâng cao.
Về phía ngoài của hình bình hành ABCD dựng các hình vuông có cạnh lần lượt là AB, BC, CD, DA. Chứng minh rằng bốn tâm của bốn hình vuông đó là đỉnh của một hình vuông.
-

Câu 45 trang 12 Sách bài tập Hình Học 11 nâng cao.
Chứng minh rằng tâm của bốn hình vuông đó làm thành một tứ giác có hai đường chéo bằng nhau và vuông góc với nhau.
-

Câu 46 trang 12 Sách bài tập Hình Học 11 nâng cao.
Gọi X, Y, Z lần lượt là trung điểm của các đoạn thẳng AB, BC, AC.

 Tải ngay
Tải ngay

