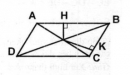
Câu 4.3 trang 162 Sách bài tập (SBT) Toán 8 tập 1Tính diện tích của tứ giác ABMD theo S Cho hình bình hành ABCD có diện tích S. Trên cạnh BC lấy hai điểm M, N sao cho BM = MN = NC = \({1 \over 3}\)BC a. Tính diện tích của tứ giác ABMD theo S b. Từ điểm N kẻ NT song song với AB (T thuộc AC). Tính diện tích của tứ giác ABNT theo S Giải:
a. ∆ DMC có CM = \({2 \over 3}\)BC Hình bình hành ABCD và ∆ DMC có chung đường cao kẻ từ đỉnh D đến BC. Gọi độ dài đường cao là h, BC = a Ta có diện tích hình bình hành ABCD là S = a h \(\eqalign{ & {S_{DMC}} = {1 \over 2}h.{2 \over 3}a = {1 \over 3}ah = {1 \over 3}S \cr & {S_{ABMD}} = {S_{ABCD}} - {S_{DMC}} = S - {1 \over 3}S = {2 \over 3}S \cr} \) b. \({S_{ABC}} = {1 \over 2}{S_{ABCD}} = {S \over 2}\) \(CN = {1 \over 3}BC\), NT // AB. Theo tính chất đường thẳng song song cách đều \( \Rightarrow CT = {1 \over 3}AC\) ∆ ABC và ∆ BTC có chung chiều cao kẻ từ đỉnh B, đáy \(CT = {1 \over 3}AC\) \( \Rightarrow {S_{BTC}} = {1 \over 3}{S_{ABC}} = {1 \over 3}.{S \over 2} = {S \over 6}\) ∆ BTC và ∆ TNC có chung chiều cao kẻ từ đỉnh T, cạnh đáy $CN = {1 \over 3}CB$ \(\eqalign{ & \Rightarrow {S_{TNC}} = {1 \over 3}{S_{BTC}} = {1 \over 3}.{S \over 6} = {S \over {18}} \cr & \Rightarrow {S_{ABNT}} = {S_{ABC}} - {S_{TNC}} = {S \over 2} - {S \over {18}} = {{9S} \over {18}} - {S \over {18}} = {{4S} \over 9} \cr} \)
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 4. Diện tích hình thang
|
-
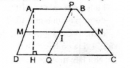
Câu 37 trang 162 Sách bài tập (SBT) Toán 8 tập 1
Chứng minh rằng mọi đường thẳng đi qua trung điểm của đường trung bình của hình thang và cắt hai đáy hình thang sẽ chia hình thang đó thành hai hình thang có diện tích bằng nhau.
-
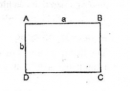
Câu 39 trang 162 Sách bài tập (SBT) Toán 8 tập 1
Tính góc nhọn của hình bình hành nếu diện tích của nó bằng một nửa diện tích của hình chữ nhật (a và b có cùng đơn vị đo)
-
Câu 40 trang 162 Sách bài tập (SBT) Toán 8 tập 1
Hai cạnh của một hình bình hành có độ dài là 6cm và 8cm. Một trong các đường cao có độ dài là 5cm. Tính độ dài đường cao thứ hai. Hỏi bài toán có mấy đáp số ?

 Tải ngay
Tải ngay