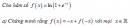Câu 4.54 trang 184 sách bài tập Giải tích 12 Nâng cao

a) Cho các số thực a, b sao cho \({{\sin a} \over 2} \ne 0\)

Với mỗi số nguyên \(n \ge 1\), xét các tổng

\(S = c{\rm{os}}b + c{\rm{os}}\left( {a + b} \right) + c{\rm{os}}\left( {2a + b} \right) + ... \)

\(+ c{\rm{os}}\left( {na + b} \right)\)

\(S = \sin b + \sin \left( {a + b} \right) + \sin \left( {2a + b} \right) + ... \)

\(+ \sin \left( {na + b} \right)\)

Tính \(S + iT\), từ đó suy ra S và T

b) Chứng minh rằng với mọi số thực \(a \ne k\pi \left( {k \in Z} \right)\), với mỗi số nguyên \(n \ge 1\)  ta có:

\(\sin a + \sin 3a + ... + \sin \left( {2n - 1} \right)a = {{{{\sin }^2}na} \over {\sin a}}\)

\({\rm{cos}}a + c{\rm{os}}3a + ... + c{\rm{os}}\left( {2n - 1} \right)a = {{\sin 2na} \over {2\sin a}}\)

Giải

a) Đặt \(\alpha  = c{\rm{os}}a + i\sin a,\beta  = \cos b + i\sin b\) thì

\(\eqalign{& S = iT = \left[ {\cos b + i\sin b} \right] \cr&+ \left[ {\cos \left( {a + b} \right) + i\sin \left( {a + b} \right)} \right]  \cr &  + \left[ {\cos \left( {2a + b} \right) + i\sin \left( {2a + b} \right)} \right] + ... \cr&+ \left[ {\cos \left( {na + b} \right) + i\sin \left( {na + b} \right)} \right] \cr} \)

\( = \beta  + \beta \alpha  + \beta {\alpha ^2} + ... + \beta {\alpha ^n}\)

\( = \beta \left( {1\alpha  + {\alpha ^2} + ... + {\alpha ^n}} \right)\)

\( = \beta {{1 + {\alpha ^{n + 1}}} \over {1 - \alpha }}\) (để ý rằng \(\alpha  \ne 1\) do \(\sin {a \over 2} \ne 0\))

\(\eqalign{&  = \beta {{1 - \cos \left( {n + 1} \right)a - i\sin \left( {n + 1} \right)a} \over {1 - \cos a - i\sin a}}  \cr &  = \beta {{\sin {{n + 1} \over 2}a} \over {\sin {a \over 2}}}\left[ {\sin {{n + 1} \over 2}a - i\cos {{n + 1} \over 2}a} \right].\cr&\;\;\;\;\;\left[ {\sin {a \over 2} + ic{\rm{os}}{a \over 2}} \right]  \cr &  = \beta {{\sin {{n + 1} \over 2}a} \over {\sin {a \over 2}}}\left( {\cos {{na} \over 2} + i\sin {{na} \over 2}} \right)  \cr &  = {{\sin {{n + 1} \over 2}a} \over {\sin {a \over 2}}}\left( {\cos {{na} \over 2} + i\sin {{na} \over 2}} \right)\left( {\cos b + i\sin b} \right)  \cr &  = {{\sin {{n + 1} \over 2}a} \over {\sin {a \over 2}}}\left[ {\cos \left( {{{na} \over 2} + b} \right) + i\sin \left( {{{na} \over 2} + b} \right)} \right] \cr} \)

Từ đó suy ra: \(S = {{\sin {{n + 1} \over 2}a} \over {\sin {a \over 2}}}\cos \left( {{{na} \over 2} + b} \right)\)  

                      \(T = {{\sin {{n + 1} \over 2}a} \over {\sin {a \over 2}}}\sin \left( {{{na} \over 2} + b} \right)\)

Chú ý: Trong phần lượng giác ở lớp 11 đã có bài tập tương tự nhưng được giải bằng cách khác.

b) Giải bằng phương pháp tương tự như câu a).

Sachbaitap.com